M9 Trigonometrie am rechtwinkligen Dreieck
Am Straßenrand sieht man oft Verkehrszeichen, die Auf eine Steigung oder ein Gefälle hinweisen.
Bei der Behandlung der linearen Funktionen und ihrer Graphen hatten wir bereits den Begriff der Steigung. 12% Steigung bedeutet, dass pro 100 m in waagerechter Richtung die Höhe um 12 m zunimmt.
Aus der Geometrie würde man Steigung eher mit einem Winkel verbinden. Unter welchem Winkel ist die Gerade gegen die Waagrechte?
tan(45°)= 1
tan(60°)= 1,732...
tan (15°)=0,2679...
tan(80°)=5,6712...
tan(30°)=0,5773...
Beispiele
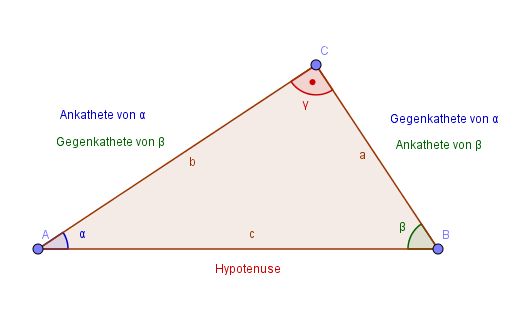
Von einem rechtwinkligen Dreieck kennt man
1. die Längen der Katheten a = 5m und b = 7m. Wie groß sind die Innenwinkel des Dreiecks?
Lösung: Es ist 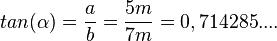 . Mit der INV-tan-Taste am TR erhält man
. Mit der INV-tan-Taste am TR erhält man 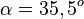
2. die Länge der Kathete a = 5m und den Winkel 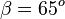 . Wie lang ist die Kathete b, die Hypotenuse c und wie groß ist der Winkel
. Wie lang ist die Kathete b, die Hypotenuse c und wie groß ist der Winkel 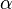 ?
?
Lösung: Es ist 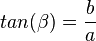 . Diese Gleichung löst man nach b auf und erhält
. Diese Gleichung löst man nach b auf und erhält 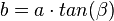 . Setzt man die Werte ein erhält man
. Setzt man die Werte ein erhält man 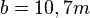 und mit dem Satz von Pythagoras
und mit dem Satz von Pythagoras 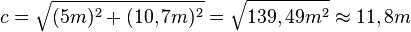 .
.
Im rechtwinkligen Dreieck ist die Summe der beiden spitzen Winkel 90°, also ist 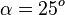
Man zeichnet das Steigungsdreieck und liest daraus ab, dass die zwei Katheten die Längen 3 und 2 haben.
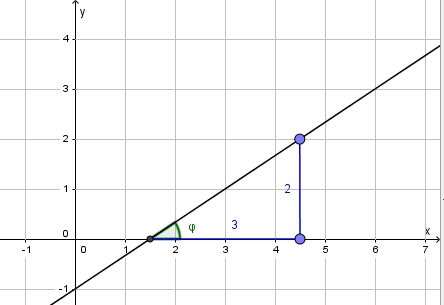
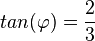 . Mit dem TR erhält man
. Mit dem TR erhält man 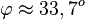 .
.


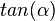 und spricht "Tangens von Alpha".
und spricht "Tangens von Alpha".
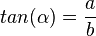 und
und  , den die Gerade
, den die Gerade 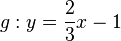 mit der x-Achse einschließt.
mit der x-Achse einschließt.


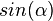 und spricht "Sinus von Alpha",
und spricht "Sinus von Alpha",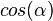 und spricht "Kosinus von Alpha".
und spricht "Kosinus von Alpha".
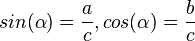 und
und 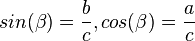 .
.

