Abstands- und Winkelbestimmungen

Dieses Thema ist im Buch auf S. 151 ausführlich beschrieben. Lesen Sie bitte diese Seite aufmerksam.

Hintergrund zur Hesseschen Normalenform:

Wir kennen die Normalenform einer Ebenengleichung. 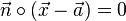$\vec{n} \circ (\vec{x} - \vec{a})=0$.
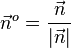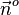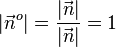Normiert man den Normalenvektoer $\vec{n}$, also $\vec{n}^o =\frac{\vec{n}}{\vert \vec{n} \vert}$, dann erhält man einen Vektor $\vec{n}^o$, der die gleiche Richtung wie der Normalenvektor $\vec{n}$ und die Länge $\vert \vec{n}^o \vert =\frac{\vert \vec{n} \vert}{\vert \vec{n} \vert}=1$ hat.