Abstands- und Winkelbestimmungen
Aus RSG-Wiki
Version vom 22. März 2020, 09:50 Uhr von Karlhaberl (Diskussion | Beiträge)
Dieses Thema ist im Buch auf S. 151 ausführlich beschrieben. Lesen Sie bitte diese Seite aufmerksam.
Hintergrund zur Hesseschen Normalenform (HNF):
Wir kennen die Normalenform einer Ebenengleichung. 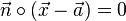 .
.
Normiert man den Normalenvektoer  , also
, also 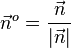 , dann erhält man einen Vektor
, dann erhält man einen Vektor 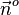 , der die gleiche Richtung wie der Normalenvektor
, der die gleiche Richtung wie der Normalenvektor  und die Länge
und die Länge 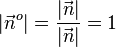 hat.
hat.
Mit dem Vektor 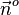 erstellt man ebenso eine Normalenform
erstellt man ebenso eine Normalenform 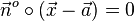 der Ebene. Man kann dies umformen und in Koordinatenschreibweise angeben:
der Ebene. Man kann dies umformen und in Koordinatenschreibweise angeben:
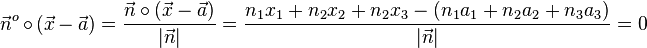
Für die Hessesche Normalform (HNF) muss außerdem gelten, dass 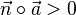 ist. Das ist so festgelegt. In der HNF in Koordinatenschreibweise muss also vor der Konstanten
ist. Das ist so festgelegt. In der HNF in Koordinatenschreibweise muss also vor der Konstanten 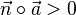 ein Minuszeichen stehen!
ein Minuszeichen stehen!
a) 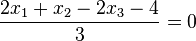
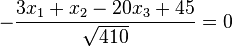 Beachten Sie das Minuszeichen vor dem Bruch. Man kann dieses Minuszeichen in den Zähler bringen und hat dann diese HNF
Beachten Sie das Minuszeichen vor dem Bruch. Man kann dieses Minuszeichen in den Zähler bringen und hat dann diese HNF 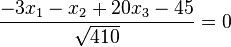
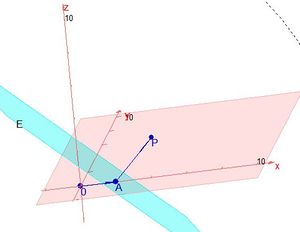
Man sieht, dass beide Vektoren vom Urprung aus in die gleiche durch die Ebene E erzeugte Halbebene zeigen.  und
und 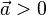 haben in etwa "die gleiche Richtung", das Skalarprodukt ist positiv.
haben in etwa "die gleiche Richtung", das Skalarprodukt ist positiv.
 und
und 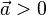 haben in etwa "die gleiche Richtung", das Skalarprodukt ist positiv.
haben in etwa "die gleiche Richtung", das Skalarprodukt ist positiv.Die Festlegung
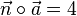 , positiv.
, positiv.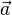 . Hier ist der Normalenvektor Fehler beim Parsen(Syntaxfehler): \vec{n} = }vec{AP}
. Hier ist der Normalenvektor Fehler beim Parsen(Syntaxfehler): \vec{n} = }vec{AP}