M8 Term und Graph bei gebrochen-rationalen Funktionen
Aus RSG-Wiki
Version vom 18. Juni 2020, 07:05 Uhr von Karlhaberl (Diskussion | Beiträge)
Auf dieser Seite soll der Zusammenhang zwischen dem Graphen und dem Funktionsterm einer gebrochen-rationalen Funktion näher untersucht werden. Dabei geht es um zwei Fragestellungen:
1. Wie finde ich aus einem gegebenen Graphen den passenden Funktionsterm.
2. Wie kann man "leicht" aus einem gegebenen Funktionsterm den Graphen angeben.
Zur Beantwortung sind die folgenden Eigenschaften gebrochen-rationaler Funktionen hilfreich.
Ausgangspunkt unserer Betrachtungen ist die indirekte Proportionalität 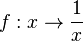 . Die Funktion ist für
. Die Funktion ist für 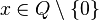 definiert. Die Funktionsgleichung ist
definiert. Die Funktionsgleichung ist 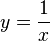 und der Funktionsgraph
und der Funktionsgraph
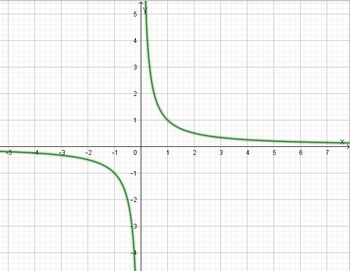
Inhaltsverzeichnis |

