M9 Anwendungen und Aufgaben zu quadratischen Gleichungen
Bruchgleichungen
Bei den Bruchgleichungen der 8. Klasse hast du schon Gleichungen wie 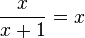 gelöst. Als Lösung hast du x=0 erhalten. Das konntest du lösen. Aber bei einer Gleichung wie
gelöst. Als Lösung hast du x=0 erhalten. Das konntest du lösen. Aber bei einer Gleichung wie 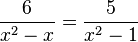 mit der Definitionsmenge D = R\{-1;0;1} gab es schon Probleme. Wie löse ich dies?
mit der Definitionsmenge D = R\{-1;0;1} gab es schon Probleme. Wie löse ich dies?
Wenn du die Bruchgleilchung 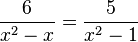 mit dem Produkt der Nenner (x2-x)(x2-1) multiplizierst, dann erhältst du:
mit dem Produkt der Nenner (x2-x)(x2-1) multiplizierst, dann erhältst du:
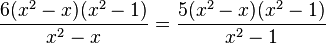 und gekürzt:
und gekürzt:
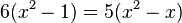
Man kann nun zusammenfassen und vereinfachen: 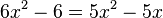 -->
--> 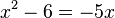 -->
--> 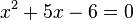 das ist eine quadratische Gleichung, die du lösen kannst.
das ist eine quadratische Gleichung, die du lösen kannst.
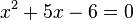 hat die Lösungen
hat die Lösungen 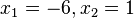 . Allerdings ist
. Allerdings ist 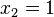 nicht in der Definitionsmenge, also ist L={-6}.
nicht in der Definitionsmenge, also ist L={-6}.
{{Lösung versteckt|1=Man verwendet den neben der Aufgabe stehende Tipp. Man multipliziert die Gleichung zuerst mit dem Hauptnenner.
a) D=R\{-1;1}, HN=(n-1)(n+1)
n+1 + n-1 = n², also n²-2n=0, n1=0, n2=2
b) D=R\{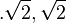 }, HN = (x+
}, HN = (x+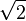 )(x-
)(x-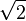 )
)
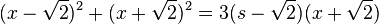
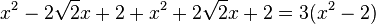
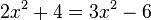
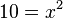 , also L={
, also L={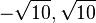 }
}
c) D=R\{-1;1} (3. binomische Formel x²-1=(x-1)(x+1)!) HN = Fehler beim Parsen(Lexikalischer Fehler): x^2-1<br> x(x+1)-(15-x)=0 --> x² +2x -15 = 0 --> x<sub>1</sub>=-5; x<sub>2</sub>=3 }} =Anwendungsaufgaben=

