M11 Aufgaben und Anwendungen der Vektorrechnung
[Lösung anzeigen][Lösung ausblenden]
1. Gesucht sind die Punktkoordinaten, diese werden waagrecht an den Punktnamen angefügt.
A(6;0;0); B(6;12;0), C(0;12;0), D(0;0;0), E(6;0;7), F(6;12;7), G(0;12;7), H(0;0;7)
M1 ist der Schnittpunkt der Flächendiagonale der unteren Fläche. Für den Ortsvektor 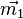 des Mittelpunktes der Strecke [DB] hat man die Formel
des Mittelpunktes der Strecke [DB] hat man die Formel 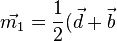 . Dies liefert dann aie Koordinaten des Schnittpunktes.
. Dies liefert dann aie Koordinaten des Schnittpunktes.
M1(3;6;0), M3(3;12;3,5), M6(3;6;7) und M(3;6;3,5)
4. a) 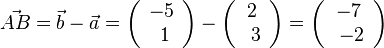 und
und 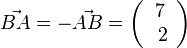
b) 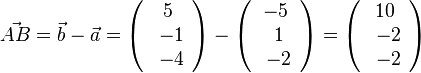 und
und 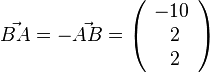
c) 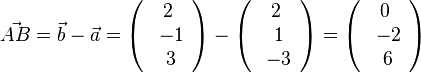 und
und 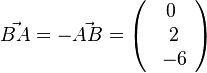
5. In dem gezeichneten Koordinatensystem im Buch ist keine Achsenskalierung angegeben. Für die Angaben wurden jeweils zwei Kästchen als 1 LE angenommen.
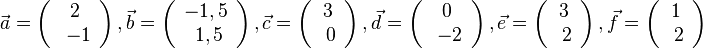
a) 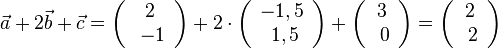
b) 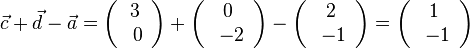
c) 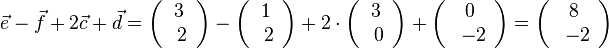
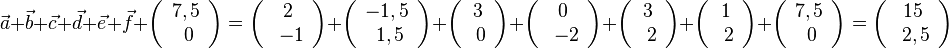
[Lösung anzeigen][Lösung ausblenden]
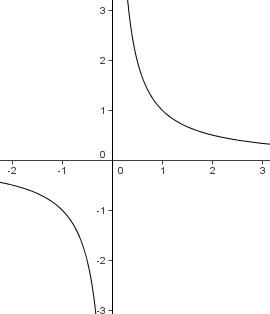
Ausgangspunkt ist die Funktion 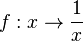 D=R\{0},
D=R\{0},
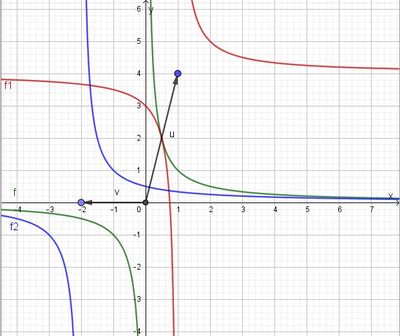
Die Definitionslücke ist bei x = 0. Die beiden Hyperbeläste sind punktsymmetrisch zum Ursprung.
a) Die Funktion 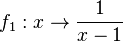 hat die Definitionslücke bei x = 1. Also wird der Graph der Funktion
hat die Definitionslücke bei x = 1. Also wird der Graph der Funktion  um 1 nach rechts in x-Richtung verschoben.
um 1 nach rechts in x-Richtung verschoben.
Zu jedem Funktionswert wird 4 addiert. Also wird zusätzlich noch in y-Richtung um 4 nach oben verschoben.
Das Symmetriezentrum ist nun (1;4) und der Verschiebungsvektor 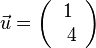 . Der grüne Graph der Funktion
. Der grüne Graph der Funktion  wird um 1 nach rechts und 4 nach oben verschoben. Man erhält den roten Graph der Funktion
wird um 1 nach rechts und 4 nach oben verschoben. Man erhält den roten Graph der Funktion 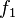 .
.
b) Die Funktion 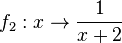 hat die Definitionslücke bei x = -2. Also wird der Graph der Funktion
hat die Definitionslücke bei x = -2. Also wird der Graph der Funktion  um -2 in x-Richtung (um 2 nach links) verschoben.
um -2 in x-Richtung (um 2 nach links) verschoben.
In y-Richtung passiert nichts.
Das Symmetriezentrum ist nun (-2;0) und der Verschiebungsvektor 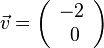 . Der grüne Graph der Funktion
. Der grüne Graph der Funktion  wird um 2 nach links verschoben und man erhält den blauen Graph der Funktion
wird um 2 nach links verschoben und man erhält den blauen Graph der Funktion 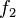 .
.
[Lösung anzeigen][Lösung ausblenden]
1a) ![\vec m = \frac{1}{2}(\vec a + \vec b) = \frac{1}{2} \cdot \left [ \left ( \begin{array}{c} 0 \\\ 3 \\\ -4 \end{array}\right) + \left ( \begin{array}{c} -6 \\\ 1 \\\ -2 \end{array}\right) \right ] = \left ( \begin{array}{c} -3 \\\ 2 \\\ -3 \end{array}\right)](/images/math/2/3/2/232ed63bc2c5edc99385002362086b10.png)
b) ![\vec m = \frac{1}{2}(\vec a + \vec b) = \frac{1}{2} \cdot \left [ \left ( \begin{array}{c} 8 \\\ 0,5 \\\ -5 \end{array}\right) + \left ( \begin{array}{c} -3 \\\ 1,5 \\\ -1 \end{array}\right) \right ] = \left ( \begin{array}{c} 2,5 \\\ 1 \\\ -3 \end{array}\right)](/images/math/2/1/d/21dc216569e9be01268e6810879107c2.png) und M(2,5;1;-3)
und M(2,5;1;-3)
![\vec s=\frac{1}{3}(\vec a + \vec b + \vec c) = \frac{1}{3} \left [ \left ( \begin{array}{c} -2 \\\ 0 \\\ 3 \end{array}\right) + \left ( \begin{array}{c} 5 \\\ 2 \\\ 1 \end{array}\right) + \left ( \begin{array}{c} 0 \\\ 4 \\\ 2 \end{array}\right) \right ]= \frac{1}{3} \left ( \begin{array}{c} 3 \\\ 6 \\\ 6 \end{array}\right) = \left ( \begin{array}{c} 1 \\\ 2 \\\ 2 \end{array}\right)](/images/math/1/3/0/130511978b9e104386eecb504758b6fc.png) und S(1;2;2)
und S(1;2;2)
[Lösung anzeigen][Lösung ausblenden]
Das Viereck ABCD bildet die Grundfläche der Pyramide. Da in der Volumenformel der Pyramide 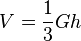 der Flächeninhalt der Grundfläche vorkommt. soll zuerst G berechnet werden.
der Flächeninhalt der Grundfläche vorkommt. soll zuerst G berechnet werden.
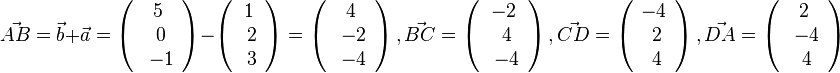
Hier sieht man, dass 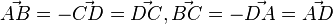 ist, das Viereck ist also ein Parallelogramm. Es ist weiterhin
ist, das Viereck ist also ein Parallelogramm. Es ist weiterhin 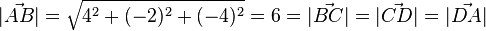 . Also ist das Viereck eine Raute.
. Also ist das Viereck eine Raute.
Wegen 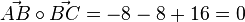 ist der Winkel bei B ein 90o-Winkel. Also ist das Viereck ein Quadrat. Sein Flächeninhalt ist dann G = 36.
ist der Winkel bei B ein 90o-Winkel. Also ist das Viereck ein Quadrat. Sein Flächeninhalt ist dann G = 36.
Aus der Volumenformel 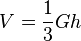 kann man nun die Länge der Pyramidenhöhe h bestimmen.
kann man nun die Länge der Pyramidenhöhe h bestimmen. 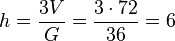 .
.
Mit dem Vektorprodukt hätte man auch den Flächeninhalt der Grundfläche G bestimmen können. Man erhält auch hier 36 (wird weiter unten noch berechnet).
Der Mittelpunkt M des Quadrats ist der Höhenfußpunkt der Pyramide. M ist auch der Schnittpunkt der Diagonalen des Quadrats, bzw. der Mittelpunkt einer Quadratdiagonalen.
Es ist ![\vec m = \frac{1}{2}(\vec a + \vec c)=\frac{1}{2} \left[ \left ( \begin{array}{c} 1 \\\ 2 \\\ 3 \end{array}\right) + \left ( \begin{array}{c} 3 \\\ 4 \\\ -5 \end{array}\right) \right ] = \left ( \begin{array}{c} 2 \\\ 3 \\\ -1 \end{array}\right)](/images/math/6/0/3/603cf07814d38f9e69600a54a9e4eb0c.png) und M(2;3;-1).
und M(2;3;-1).
Nun muss man senkrecht zu G von M aus 6 Einheiten nach "oben" oder "unten" gehen um zu S zu kommen. Dazu braucht man einen Vektor 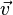 , der senkrecht zur Grundfläche steht. Einen solchen Vektor erhält man, wenn man das Vektorprodukt
, der senkrecht zur Grundfläche steht. Einen solchen Vektor erhält man, wenn man das Vektorprodukt 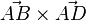 bestimmt. Es ist
bestimmt. Es ist 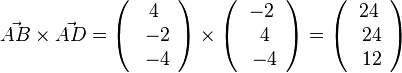
Der Betrag des Vektors 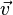 ist
ist 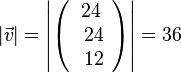
Der Einheitsvektor zu 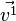 zum Vektor
zum Vektor 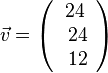 ist
ist 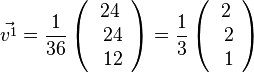
Nun muss man die Pyramidenspitze S bestimmen. Von M aus geht man 6 Einheiten in Richtung des Einheitsvektors 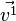 , also
, also 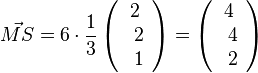 .
.
Die Spitze S hat den Ortsvektor 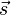 und es ist
und es ist 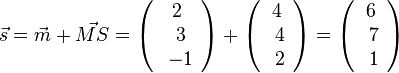 und S(6;7;1)
und S(6;7;1)
Man hätte von M aus auch in die Richtung von 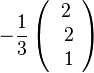 gehen können. Dann geht man von M aus 6 Einheiten in Richtung dieses Einheitsvektors und bekommt dann
gehen können. Dann geht man von M aus 6 Einheiten in Richtung dieses Einheitsvektors und bekommt dann 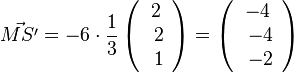 .
.
[Lösung anzeigen][Lösung ausblenden]

