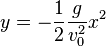Ph10 Der waagrechte Wurf
Aus RSG-Wiki
Version vom 2. März 2021, 14:06 Uhr von Karlhaberl (Diskussion | Beiträge)
|
Merke:
Der waagrechte Wurf ist eine zweidimensionale Bewegung und setzt sich als Überlagerung
zusammen. |
Bei einem waagrechter Wurf wirft man einen Körper waagrecht mit einer Anfangsgeschwindigkeit los. Er fliegt dann geradlinigen in x-Richtung mit konstanter Geschwindigkeit weiter, gleichzeitig wirkt auf ihn seine Gewichtskraft in y-Richtung. Von dieser wird er mit konstanter Beschleunigung nach unten beschleunigt (freier Fall).
Beispielaufgabe:

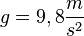 nach unten
nach unten