M11 Die Kettenregel
Die Ableitung einer Funktion  , die die Verkettung der Funktionen
, die die Verkettung der Funktionen  und
und  ist, erhält man mit der Kettenregel. Es ist
ist, erhält man mit der Kettenregel. Es ist 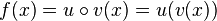 .
.
Nach der Definition der Ableitung ist 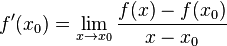 .
.
Nun muss man dabei beachten was die Funktionen  und
und  dabei machen.
dabei machen.
Wenn 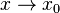 ist, dann ist
ist, dann ist 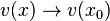 .
.
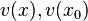 sind die Argumente, die in u eingesetzt werden. Dabei ist dann, wenn
sind die Argumente, die in u eingesetzt werden. Dabei ist dann, wenn 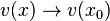 ist , auch
ist , auch 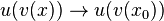 .
.
Damit kann man den Differenzenquotienten schreiben:
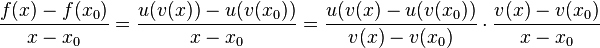 .
.
Beim letzten Term stimmt der Nenner des ersten Bruches mit den Zähler des 2. Bruches überein.
Der erste Bruch 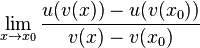 bedeutet, dass man
bedeutet, dass man  nach
nach 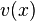 ableitet und der zweite Bruch
ableitet und der zweite Bruch 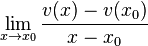 bedeutet, dass man
bedeutet, dass man  nach
nach 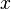 ableitet.
ableitet.
Also hat man 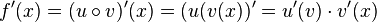 .
.
|
Merke:
Kettenregel
Man leitet zuerst die äußere Funktion ab und multipliziert mit der Ableitung der inneren Funktion. Dies nennt man Nachdifferenzieren. |
Beispiele:
1.Wir nehmen das Anfangsbeispiel der Seite M11_Verkettung_von_Funktionen
Es ist 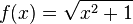 . Dabei ist
. Dabei ist 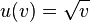 die Funktionsgleichung der äußeren Funktion. Das Argument der Funktion
die Funktionsgleichung der äußeren Funktion. Das Argument der Funktion  wurde mit
wurde mit  bezeichnet, damit man sieht, dass die Variable von
bezeichnet, damit man sieht, dass die Variable von  nun
nun  (eigentlich
(eigentlich 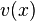 ) ist.
) ist.
Die innere Funktion hat die Funktionsgleichung 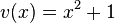 .
.
Für die Ableitung 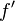 der Funktion
der Funktion  differenziert man die äußere Funktion
differenziert man die äußere Funktion  nach
nach  . Also ist
. Also ist 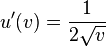 und multipliziert dieses Ergebnis mit der Ableitung der inneren Funktion
und multipliziert dieses Ergebnis mit der Ableitung der inneren Funktion  nach
nach 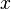 , also mit
, also mit 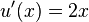 .
.
Insgesamt erhält man nun 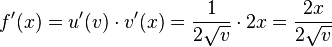 . Nun ersetzt man wieder
. Nun ersetzt man wieder  durch
durch 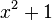 und kürzt 2, dann ist das Ergebnis
und kürzt 2, dann ist das Ergebnis
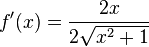 .
.2.  mit
mit 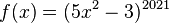 ist die Verkettung der Funktion
ist die Verkettung der Funktion  mit
mit 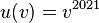 mit der Funktion
mit der Funktion  mit
mit 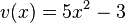 .
.
Die Ableitung von 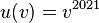 ist
ist 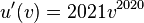 (Ableitung der äußeren Funktion)
(Ableitung der äußeren Funktion)
und die Ableitung von 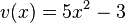 ist
ist 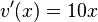 (Ableitung der inneren Funktion).
(Ableitung der inneren Funktion).
Die Ableitungsfunktion 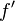 erhält man durch
erhält man durch 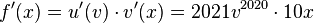 .
.
Nun ersetzt man weider  durch
durch 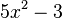 und hat dann die Ableitung der Funktion
und hat dann die Ableitung der Funktion 
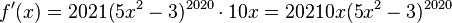 .
.Und das ging doch deutlich besser als die Potenz 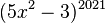 auszurechnen und ein Polynom vom Grad 2021 abzuleiten!
auszurechnen und ein Polynom vom Grad 2021 abzuleiten!
Man kann die Schreibweise auch verkürzen, indem man die Schreibweise mit "v" weglässt und gleich nur mit den Funktionen von x schreibt. Dabei wird gleich v durch den Funktionsterm v(x) ersetzt.
Das Beispiel 1 ergibt dann  .
.
Das Beispiel 2 schreibt sich dann 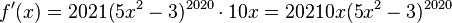 .
.
Schauen Sie sich auch die Beispiele 2 bis 4 im Buch auf S. 130 an. Beim Beispiel 3 kann man das Quadrat ausrechnen und ableiten. Man erhält das gleiche Ergebnis, wie wenn man den ursprünglichen Term mit der Kettenregel ableitet.
Das Beispiel 4 verdeutlicht die Auswirkung auf die Definitionsmenge, was sehr selten vorkommt.
|
Als sehr praktikabel hat sich dieses Verfahren erwiesen:
In unseren Beispielen: |

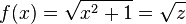 mit
mit 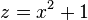 .
.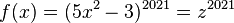 mit
mit 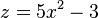 .
.
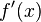 ergibt sich dann durch
ergibt sich dann durch 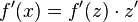 .
.
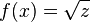 ergibt
ergibt 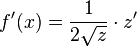 und dann ersetzt man für z durch
und dann ersetzt man für z durch 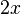 , also
, also 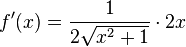 .
.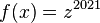 ergibt
ergibt 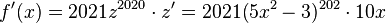 .
.
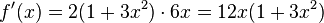 und
und 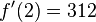
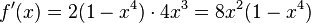 und
und 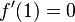
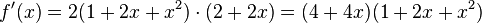 und
und 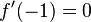
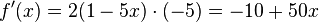 und
und 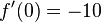
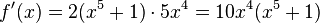 und
und 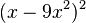 ab.
ab.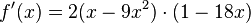 und
und 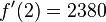
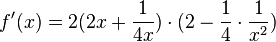 und
und 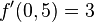
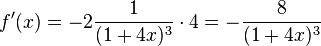 und
und 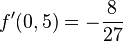
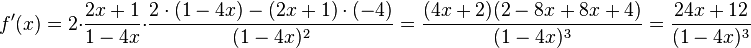 und
und 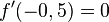
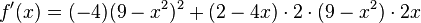 und
und 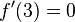
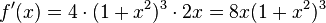 und
und 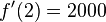
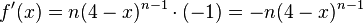 und
und 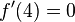
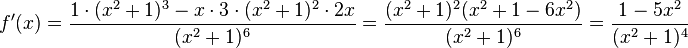 und
und 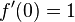
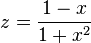 und
und 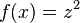 .
.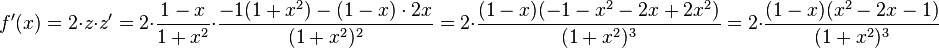 und
und 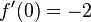
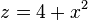 und
und 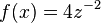
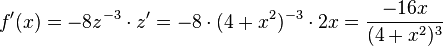 und
und 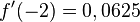
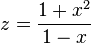 und
und 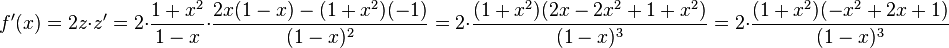 und
und 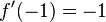
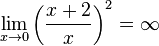
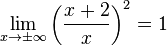 , da der Grad des Zählerpolynoms = Grad des Nennerpolynoms ist und der Quotient der Koeffizienten von x 1 ist.
, da der Grad des Zählerpolynoms = Grad des Nennerpolynoms ist und der Quotient der Koeffizienten von x 1 ist. 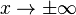 .
.
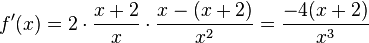
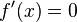 wenn x = -2 ist.
wenn x = -2 ist. 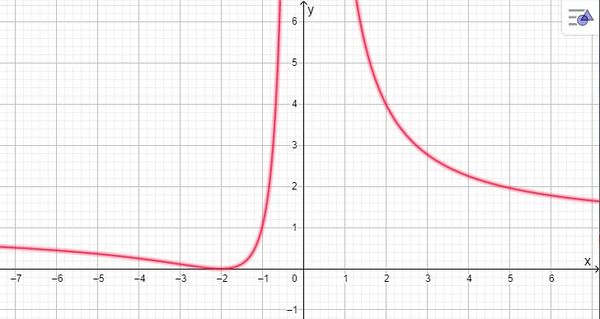
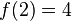 und
und 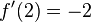
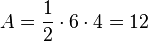 .
.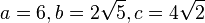 und
und 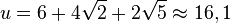
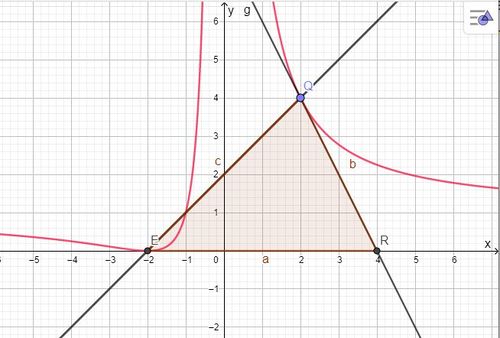
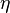 im Dreieck QER ist bei E. Es ist
im Dreieck QER ist bei E. Es ist 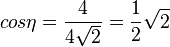 (im rechtwinkligen Dreieck ABF, wenn F der Höhenfusspunkt ist), also
(im rechtwinkligen Dreieck ABF, wenn F der Höhenfusspunkt ist), also 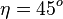 .
.
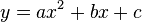 und setzt die Koordinaten der drei Punkte E, R und Q ein. Man erhält drei Gleichungen mit drei Unbekannten a, b, c.
und setzt die Koordinaten der drei Punkte E, R und Q ein. Man erhält drei Gleichungen mit drei Unbekannten a, b, c.