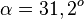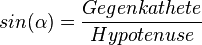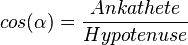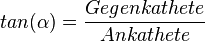M9 Aufgaben zur Trigonometrie am rechtwinkligen Dreieck
30px Merke
Sinus, Kosinus und Tangens kannst du nur in rechtwinkligen Dreiecken verwenden. Also suche dir bei den Aufgaben passende rechtwinklige Dreiecke, bei denen 2 Größen gegeben sind und rechne dann mit einer dieser Gleichungen
die Unbekannte aus. |
Buch S. 129 / 10
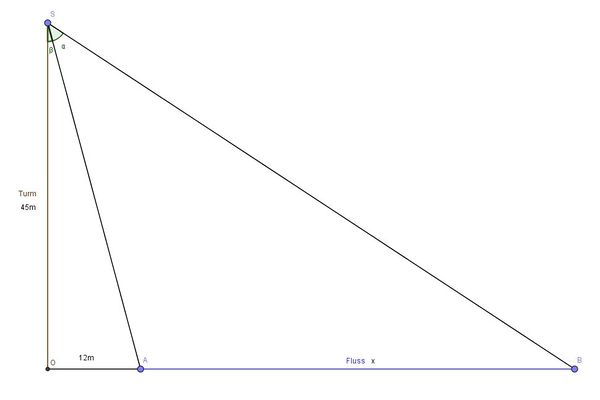
Das Dreieck SOA ist rechtwinklig. Zum Winkel 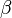 kennt man die Gegenkathete 12m und die Ankathete 45m. Also erhält man mit
kennt man die Gegenkathete 12m und die Ankathete 45m. Also erhält man mit 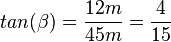 den Winkel
den Winkel 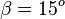 .
.
Nun kennt man im rechtwinkligen Dreieck SOB den Winkel 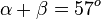 und seine Ankathete 45m. Die Gegenkathete ist 12m + x. In dem Dreieck SOB ist also
und seine Ankathete 45m. Die Gegenkathete ist 12m + x. In dem Dreieck SOB ist also 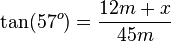 .
.
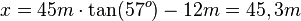
Buch S. 129 / 11
a)
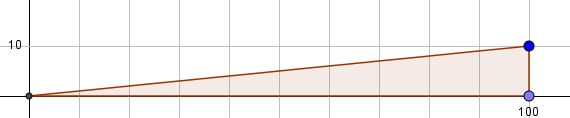
Das gezeichnete Dreieck ist bei 100 rechtwinklig. Gesucht ist der Winkel zwischen der x-Achse und der Geraden. Die Gegenkathete des Winkels ist im Bild 10. Also hat man für den Winkel An- und Gegenkathete. Damit ist 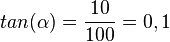 und
und 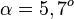
b) 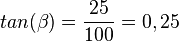 und
und 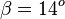
c) 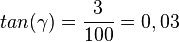 und
und 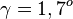
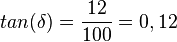 und
und 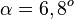
Buch S. 129 / 13
a) Angaben: Es ist 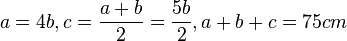 .
.
Setzt man für a und c die Terme aus den ersten beiden Gleichungen in die dritte Gleichung ein, so erhält man 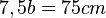 und
und 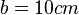 .
.
a = 40cm, b = 10cm, c = 25cm
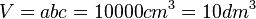 und
und 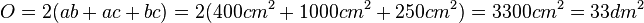
b) Die Länge der Flächendiagonale [AC] erhält man mit dem Satz von Pythagoras 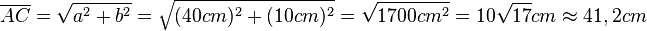
Die Länge der Raumdiagonale [AG] erhält man als Folge des Satzes von Pythagoras 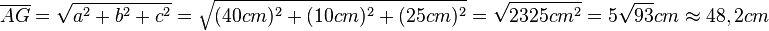
In dem rechtwinkligen Dreieck ACG ist 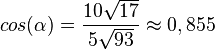 und
und 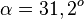
Den Winkel hätte man auch mit Sinus oder Tangens berechnen können.
Es ist 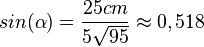 und
und 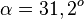
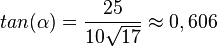 und
und