M9 Aufgaben zur Trigonometrie
Ordne richtig zu
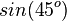 |
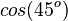
|
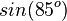 |
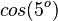
|
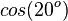 |
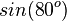
|
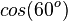 |
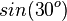
|
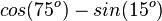 |
0 |
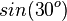 |
0,5 |
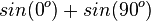 |
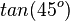
|
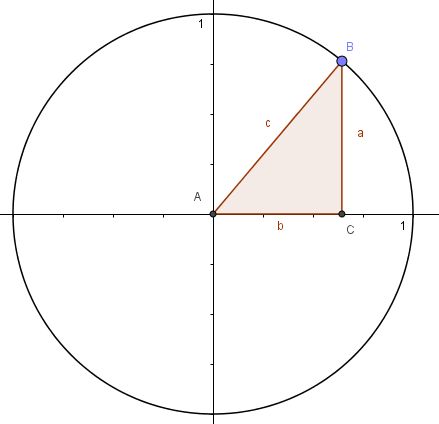
1. Es ist c = 1, da c ein Radius ist.
2. 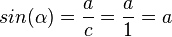
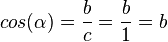
3. 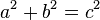
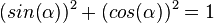
|
Merke:
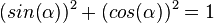 |
1. 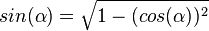 ,
, 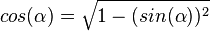
2. a)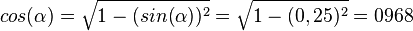
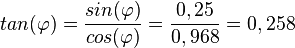
b) 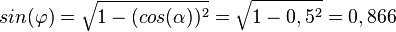
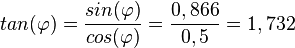
c) 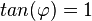 bedeutet
bedeutet 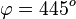 und
und 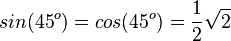
d) 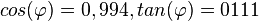
e) 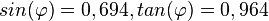
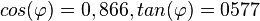
a) Im Dreieck sind An- und Gegenkathete zum Winkel  . Also
. Also 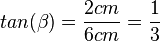 ergibt
ergibt 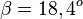 .
.
b) Zum Winkel 25o ist die Hypotenuse gegeben. Gesucht ist seine Gegenkathete. Also 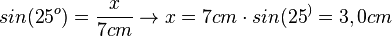 .
.
c) Im Dreieck sind Ankathete und Hypotenuse zum Winkel 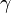 . Also
. Also 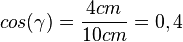 ergibt
ergibt 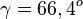 .
.
d) Hier hat man zwei rechtwinklige Dreiecke. Eines mit den Seiten z1, y und 12cm, das andere mit den Seiten z2, x und 12cm.
Im ersten Dreieck (mit den Seiten z1, y und 12cm) ist zum Winkel 60o die Gegenkathete gegeben. Dann kann man die Hypotenuse y mit dem Sinus berechnen. 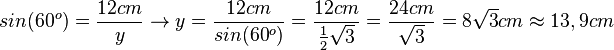
In diesem Dreieck ist auch noch die Ankathete zum 60o-Winkel gesucht. Hier kann man sich aussuchen, ob man mit cos oder tan rechnen will. 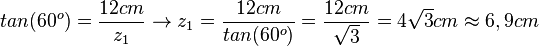 oder
oder 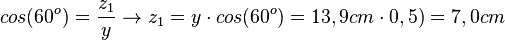 . Die unterschiedlichen Ergebnisse 6,9 cm und 7,0cm ergeben sich aus den Rundungen, mit denen man weiterrechnet. Wenn man die gnaze Anzeige des Taschenrechners nimmt und mit ihr weiterrechnet, erhält man in beiden Fällen 6,9cm.
. Die unterschiedlichen Ergebnisse 6,9 cm und 7,0cm ergeben sich aus den Rundungen, mit denen man weiterrechnet. Wenn man die gnaze Anzeige des Taschenrechners nimmt und mit ihr weiterrechnet, erhält man in beiden Fällen 6,9cm.
Im zweiten Dreieck (mit den Seiten z2, x und 12cm) geht man ähnlich vor.
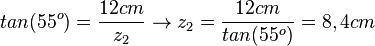 ,
,
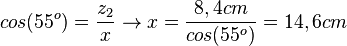
e) Auch hier hat man zwei Dreiecke. Im linken Dreieck ist zum 12o-Winkel die Ankathete gegeben und die Hypotenuse gesucht. Also 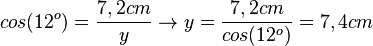
Im rechten Dreieck ist die Gegenkathete zum 12o-Winkel gesucht und die Ankathete gegeben. Also 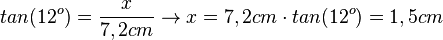
{{Lösung versteckt|1=a) Als Skizze nimmt man das rechte Dreieck. Man sieht, dass man hb berechnen kann. Es ist 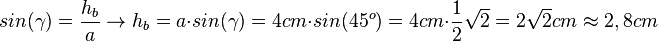
Damit ist der Flächeninhalt 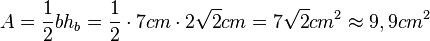
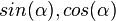 .
.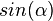 und
und 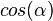 erhältst du?
erhältst du?

 für
für 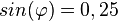 die Werte von
die Werte von 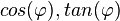 .
.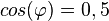 die Werte von
die Werte von 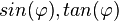 .
.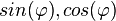 .
.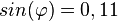 die Werte von
die Werte von 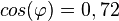 die Werte von
die Werte von 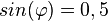 die Werte von
die Werte von 
