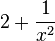M10 Symmetrie
Es gibt zwei verschiedene Arten von Symmetrien zum Koordinatensystem:
Achsensymmetrie zur y-Achse
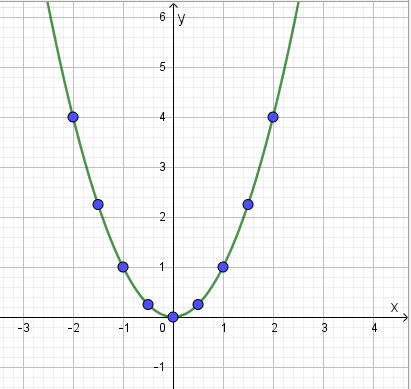
Der Graph einer Funktion f ist genau dann achsensymmetrisch zur y-Achse, wenn der Graph auf der linken Seite der y-Achse ein Spiegelbild der rechten Seite ist. Die y-Achse ist Symmetrieachse des Graphen von f.
Rechnerisch bedeutet dies, dass f(-x)=f(x) ist.
|
Merke:
Gilt für die Funktion f, dass f(-x) = f(x) ist, dann ist der Graph von f achsensymmetrisch zur y-Achse. |
Man überprüft das, indem man in den Funktionsterm von f statt x nun -x einsetzt. Wenn der Graph achsensymmetrisch zur y-Achse ist, dann muss man den gleichen Term f(x) wieder erhalten.
a) f(-x) = (-x)2 - 2 = x2 - 2 = f(x)
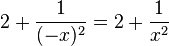 = f(x)
= f(x)
Punktsymmetrie zum Ursprung
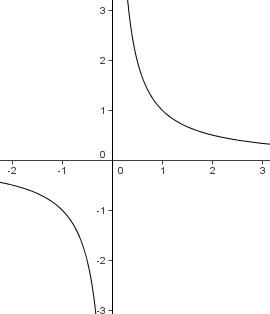
Der Graph einer Funktion f ist genau dann punktsymmetrisch zum Ursprung, wenn man ihn um 180° drehen kann und man wieder den gleichen Graph erhält. Oder macht man zwei Achsenspiegelungen an der x-Achse und an der y-Achse und erhält wieder den Graphen von f.
Rechnerisch bedeutet dies, dass f(-x)= - f(x) ist.
|
Merke:
Gilt für die Funktion f, dass f(-x) = - f(x) ist, dann ist der Graph von f punktsymmetrisch zum Ursprung y-Achse. |
Man überprüft das, indem man in den Funktionsterm von f statt x nun -x einsetzt. Wenn der Graph achsensymmetrisch zur y-Achse ist, dann muss man den gleichen Term f(x) wieder erhalten.
a) f(-x) = -x = - f(x)
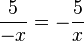 = - f(x)
= - f(x)Aufgaben
Ausblick
Achsensymmetrie zu einer anderen Achse und Punktsymmetrie zu einem anderen Punkt wird dir hier erklärt.