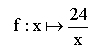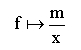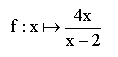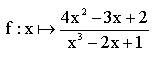Einführung

Station 1: Einführung - Station 2: Lernpfad - Station 3: Test

Eine Tafel Schokolade mit 24 Stücken soll auf Kinder verteilt werden. Wie viele Stückchen bekommt jedes Kind?

x bezeichne die Anzahl der Kinder und y die Anzahl der Schokoladenstückchen, die jedes Kind bekommt.

Aufgabe: Vervollständige die Tabelle:

Aufgabe: Zeichne den Graph für dieses Beispiel.

Betrachte die Produkte x*y, so stellst du fest, dass x*y= 24 ist.

Eine Zuordnung zwischen zwei Größen x und y heißt indirekt proportional, wenn das Produkt x*y für alle Paare (x,y) stets konstant ist.

In diesem Beispiel kann x nur eine natürliche Zahl zwischen 1 und 24 sein.

Man kann die Funktion

allgemein für alle rationalen Zahlen x, die ungleich Null sind, erklären.
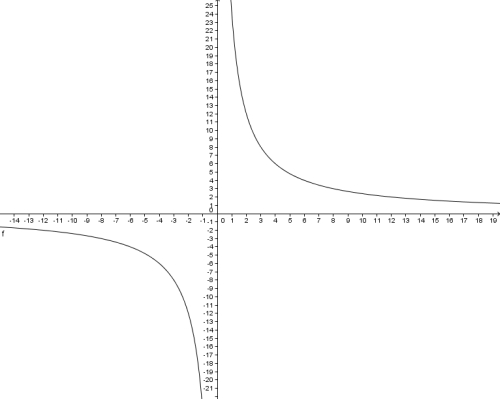
Der Graph dieser Funktion schaut dann so aus:

Der Graph einer indirekten Proportionalität heißt Hyperbel.

Die Funktion

mit einer rationalen Zahl m heißt indirekte Proportionalität oder indirekt proportionale Funktion.

Was ist Definitionsmenge, Wertemenge? Ist der Graph symmetrisch?
Lösung

Aufgaben:

1. Stelle in dieser GeoGebra-Datei den Schieberegler für m so ein, dass es den Graphen von

zeigt.

2. Beantworte die Fragen auf dieser Seite

Der Funktionsterm von

ist ein Bruch. Nun kann im Zähler und Nenner eines Bruches auch die Variable x vorkommen. Deshalb definiert man allgemein:

Ist der Funktionsterm der Funktion f ein Bruch und stehen in Nenner und/oder Zähler Terme mit der Variablen x, zum Beispiel

oder allgemeiner

so heißt diese Funktion rationale Funktion.

Navigationsmenü