Hessesche Normalenform
Wie man auf die Die Hesseschen Normalenform (HNF) kommt soll erklärt werden.
Wir kennen die Normalenform einer Ebenengleichung. 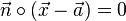 .
.
Normiert man den Normalenvektoer  , also
, also 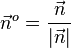 , dann erhält man einen Vektor
, dann erhält man einen Vektor 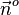 , der die gleiche Richtung wie der Normalenvektor
, der die gleiche Richtung wie der Normalenvektor  und die Länge
und die Länge 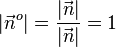 hat. Der Vektor
hat. Der Vektor 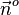 ist der Normaleneinheitsvektor.
ist der Normaleneinheitsvektor.
Mit dem Vektor 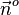 erstellt man ebenso eine Normalenform
erstellt man ebenso eine Normalenform 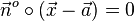 der Ebene. Man kann dies umformen und in Koordinatenschreibweise angeben:
der Ebene. Man kann dies umformen und in Koordinatenschreibweise angeben:
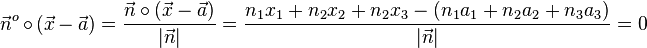
Für die Hessesche Normalform (HNF) muss außerdem gelten, dass 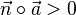 ist. Das ist so festgelegt. In der HNF in Koordinatenschreibweise muss also vor der Konstanten
ist. Das ist so festgelegt. In der HNF in Koordinatenschreibweise muss also vor der Konstanten 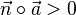 ein Minuszeichen stehen!
ein Minuszeichen stehen!
a) 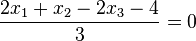
b) 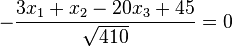
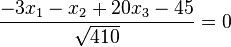
Wieso nun  ?
?
Das hat eine anschauliche Bedeutung, die Sie in den nächsten zwei Aufgaben kennenlernen.
 und
und 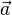 haben in etwa "die gleiche Richtung", das Skalarprodukt ist positiv.
haben in etwa "die gleiche Richtung", das Skalarprodukt ist positiv.
Die Festlegung 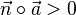 bedeutet anschaulich, dass vom Ursprung aus die
bedeutet anschaulich, dass vom Ursprung aus die  und
und 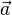 haben in etwa "die gleiche Richtung" haben.
haben in etwa "die gleiche Richtung" haben.
 und
und 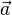 in verschiedene durch die Ebene E erzeugten Halbräume zeigen. Ihr Zwischenwinkel ist > 90°. Also ist ihr Skalarprodukt negativ und in der Normalenform steht -(-45) = 45. Dann muss man für die HNF das Vorzeichen ändern, indem man vor den Bruch ein Minuszeichen schreibt. dies ist in Aufgabe 1 erfolgt.
in verschiedene durch die Ebene E erzeugten Halbräume zeigen. Ihr Zwischenwinkel ist > 90°. Also ist ihr Skalarprodukt negativ und in der Normalenform steht -(-45) = 45. Dann muss man für die HNF das Vorzeichen ändern, indem man vor den Bruch ein Minuszeichen schreibt. dies ist in Aufgabe 1 erfolgt.
Nun zur Normierung des Normalenvektors:
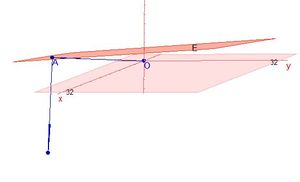
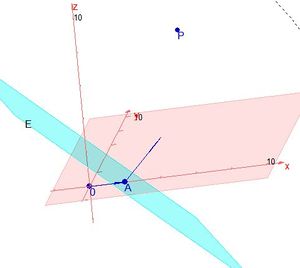
In diesem Bild ist ein Punkt P außerhalb der Ebene E gegeben. A ist in diesem Fall der Lotfußpunkt des Lotes von P auf E. (Den Lotfußpunkt erhält man, indem man von P aus in Richtung des Normalenvektors der Ebene E geht und den Schnittpunkt der Lotgeraden 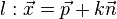 mit der Ebene E bestimmt.)
mit der Ebene E bestimmt.)
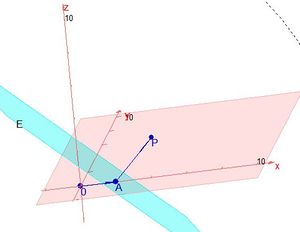
Geht man von A in Richtung P, so ist der Vektor 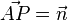 und der Punkt P hat von der Ebene E den Abstand
und der Punkt P hat von der Ebene E den Abstand 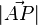 . Normiert man den Normalenvektor so erhält man
. Normiert man den Normalenvektor so erhält man 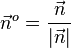 und es ist dann
und es ist dann 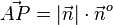 . Der Zahlenwert bei
. Der Zahlenwert bei 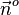 gibt dann den Abstand des Punktes P von der Ebene E an.
gibt dann den Abstand des Punktes P von der Ebene E an.
Nun ist 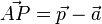 und damit
und damit 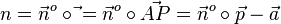 , was dem Term in der HNF entspricht.
, was dem Term in der HNF entspricht.
Dies war nun die Überlegung, wenn der Punkt P senkrecht zur Ebene E über dem Stützpunkt A liegt.
Was macht man, wenn dies nicht der Fall ist?
Die gerade ausgeführte Überlegung führt zu Abstandsbestimmung eines Punktes P von der Ebene E.
|
Merke:
Der Abstand eines Punktes P von der Ebene E ist Man erhält den Abstand, indem man in der Hesseschen Normalform den Ortsvektor |
 Der Punkt P liegt offensichtlich nicht senkrecht über A.
Der Punkt P liegt offensichtlich nicht senkrecht über A. 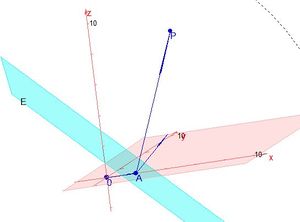
Der Vektor 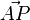 und der Normalenvektor
und der Normalenvektor  schließen nun einen Winkel ein. Dies ist der gleiche Winkel, den der Vektor
schließen nun einen Winkel ein. Dies ist der gleiche Winkel, den der Vektor 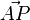 mit dem Normaleneinheitsvektor
mit dem Normaleneinheitsvektor 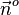 einschließt.
einschließt.
Es ist also 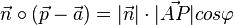 und
und
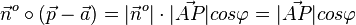 mit gleichem Winkel
mit gleichem Winkel  in beiden Formeln.
in beiden Formeln.
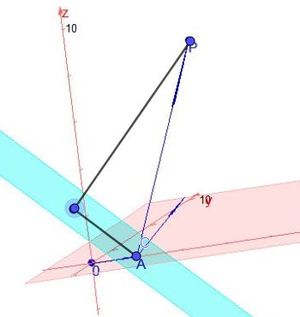
Ist L der Lotfußpunkt des Lotes von P auf die Ebene E, dann gilt im rechtwinkligen Dreieck ALP 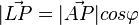 .
.
Es ist also 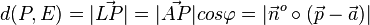
Bemerkungen:
1. Da für den Abstand 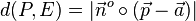 des Punktes P von der Ebene E ein Betrag die Rechnung bestimmt sind die Überlegungen zu
des Punktes P von der Ebene E ein Betrag die Rechnung bestimmt sind die Überlegungen zu 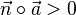 bedeutungslos, da es für die Abstandsberechnung egal ist ob man von
bedeutungslos, da es für die Abstandsberechnung egal ist ob man von 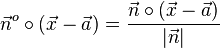 oder von
oder von 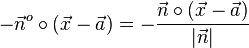 den Betrag nimmt.
den Betrag nimmt.
2. Lässt man beim Abstand 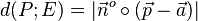 des Punktes P von der Ebene E die Betragsstriche weg, also
des Punktes P von der Ebene E die Betragsstriche weg, also 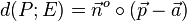 erhält man noch mehr Informationen.
erhält man noch mehr Informationen.
Für die Abstandsberechnung wird die HNF 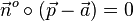 vorausgesetzt, also
vorausgesetzt, also 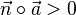 . Wenn mann dann die richtige HNF hat, statt
. Wenn mann dann die richtige HNF hat, statt 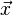
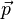 in
in 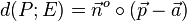 einsetzt und den Abstand des Punktes P von der Ebene E mit
einsetzt und den Abstand des Punktes P von der Ebene E mit 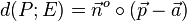 berechnet, dann kann d(P,E) auch negative Werte annehmen. Dabei bedeutet
berechnet, dann kann d(P,E) auch negative Werte annehmen. Dabei bedeutet
d(P,E) > 0, dass P und der Ursprung O in verschiedenen Halbräumen des durch E geteilten Raumes liegen.
d(P,E) = 0, dass P in E liegt.
d(P,E) < 0, dass P und der Ursprung O im gleichen Halbraum liegen.
Die Hessesche Normalenform liefert also Informationen zum Abstand und zur Lage eines Punktes P zu der Ebene E.
Zurück zu Abstands-_und_Winkelbestimmungen
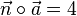 , positiv.
, positiv.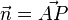 .
.