London Eye - Anwendungen von Sinus- und Kosinusfunktionen
Koproduktion Liebetanz/Heim anlässlich des Tages des digitalen Lernens

Lizenzgebührenfreies Bild - Fotograf:Frank-Michael Zink
Inhaltsverzeichnis |
Wiederholung zum Selbststudium
Einführung der trigonometrischen Funktionen
Eigenschaften trigonometrischer Funktionen
Einfluss von Parametern im Funktionsterm auf die Graphen der Sinus-und Kosinusfunktion
Die Aufgabe
Das London Eye, eine der Touristenattraktionen, Londons hat einen Durchmesser von 122 m. Die Dauer einer Umdrehung beträgt 30 Minuten. Geben Sie einen Funktionsterm h(t) mit h(0) = 0 an., der die Höhe h einer Gondel über dem Einstiegsniveeau in Abhängigkeit von der Zeit angibt.
|
Die Lösung
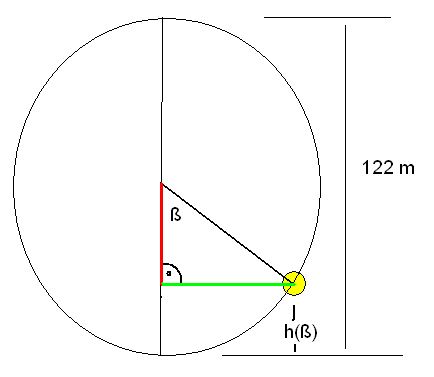
|
Arbeitsaufgaben: 1. Gib den Funktionsterm h(ß) an.(ß im Bogenmaß) |
Die Visualisierung mittels Geogebra und weiterführende Betrachtungen
Media:london11.ggb
Erstellt von Bernhard Heim
Diese Datei erfordert die Installation der Version Web-Start von Geogebra! [1]
|
Arbeitsaufgaben: Dargestellt ist die Höhe über dem Boden bei einer Rotation in 30 Minuten.
|
Media:london33.ggb
Erstellt von Bernhard Heim
Diese Datei erfordert die Installation der Version Web-Start von Geogebra! [2]
|
Arbeitsaufgaben: Dargestellt ist
|
Media:london22.ggb
Erstellt von Nathanael Liebetanz
Diese Datei erfordert die Installation der Version Web-Start von Geogebra! [3]
|
Arbeitsaufgaben: Zu erkennen ist die Geschwindigkeit des Riesenrades tangential zum Riesenrad, deren Betrag konstant ist und ihre Zerlegung in die horizontal und vertikal wirkenden Kräfte.
|

