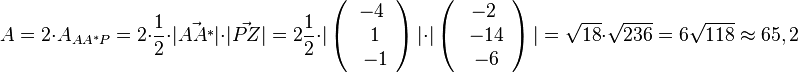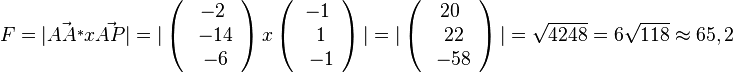Abstands- und Winkelbestimmungen
Dieses Thema ist im Buch auf S. 151 ausführlich beschrieben. Lesen Sie bitte diese Seite aufmerksam.
Die Hessesche Normalenform (HNF)
Aufgaben
S. 153/1
a) Die Ebene E hat als HNF 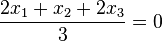 .
.
Der Ursprung O hat den Abstand von der Ebene E 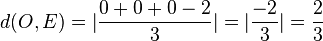 .
.
Man kann die Rechnung auch ohne Betragstriche machen. Ergibt sich ein negatives Ergebnis wie hiernimmt man hiervon den Betrag.
Der Abstand des Punktes P(6;-1;9) von der Ebene E ist 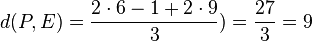
b) Die Ebene E hat als HNF 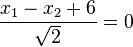 .
.
Der Ursprung O hat den Abstand von der Ebene E 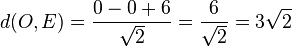 .
.
Der Punkt P(7;7;2) hat von E den Abstand 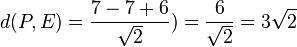 .
.
c) Die Ebene E hat als HNF 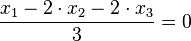 .
.
Der Ursprung O hat den Abstand von der Ebene E 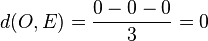 . Der Ursprung liegt in der Ebene E.
. Der Ursprung liegt in der Ebene E.
Der Punkt P(-1;1;3) hat von E den Abstand 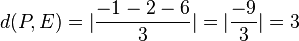 .
.
d) Die Ebene E hat als HNF 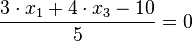 .
.
Der Ursprung O hat den Abstand von der Ebene E 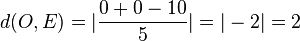 .
.
Der Punkt P(4;-1;2) hat von E den Abstand 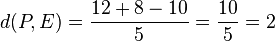 .
.
O und P liegen jeweils im Abstand 2 in verschiedenen Halbräumen zur Ebene E.
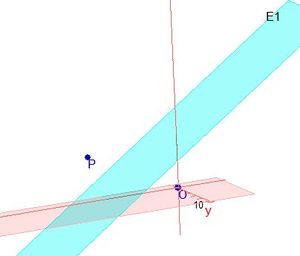
S. 153/2
(1) Wegen 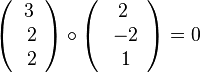 steht der Richtungsvektor
steht der Richtungsvektor 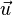 der Geraden g senkrecht zum Normalenvektor
der Geraden g senkrecht zum Normalenvektor  der Ebene E.
der Ebene E. 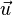 ist also komplanar zu den Richtungsvektoren der Ebene E.
ist also komplanar zu den Richtungsvektoren der Ebene E.
Die Ebene E hat als HNF 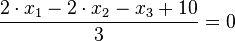 .
Für den Stützpunkt A(7;-13;-4) der Gerade g berechnet man
.
Für den Stützpunkt A(7;-13;-4) der Gerade g berechnet man 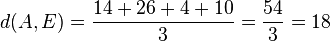 , also liegt A nicht in E und g ist echt parallel zu E. Das g echt parallel zu E ist, hat g auch den Abstand 18 zur Ebene E.
, also liegt A nicht in E und g ist echt parallel zu E. Das g echt parallel zu E ist, hat g auch den Abstand 18 zur Ebene E.
Wird g senkrecht auf E projeziert, dann wird in Richtung des Normalenvektors projeziert. Fällt man von A das Lot 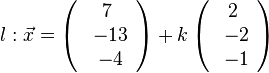 auf E, dann erhält man den Lotfusspunkt L durch 2(7+2k)-2(-13-2k)-(-4-k)+10=0 und k = -6 und L(-5;-1;2). Damit hat man für g* den Stützpunkt. Ihr Richtungsvektor ist derselbe wie bei g, da er "in E liegt" (ist komplanar zu den Richtungsvektoren von E). Die senkrechte Projektion von g in die Ebene E ist dann
auf E, dann erhält man den Lotfusspunkt L durch 2(7+2k)-2(-13-2k)-(-4-k)+10=0 und k = -6 und L(-5;-1;2). Damit hat man für g* den Stützpunkt. Ihr Richtungsvektor ist derselbe wie bei g, da er "in E liegt" (ist komplanar zu den Richtungsvektoren von E). Die senkrechte Projektion von g in die Ebene E ist dann 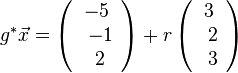 .
.
(2) Analog geht man hier vor.
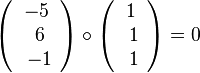 .
.
HNF von E: 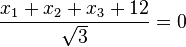 .
.
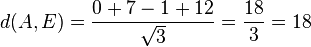
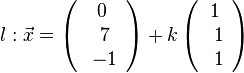
k + (7+k) + (-1+k) + 12 = 0 --> k = -6 und L(-6;1;-7)
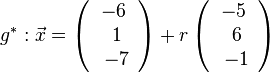
S. 154/4
Die Ebene E hat HNF 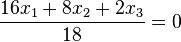 .
Für diese Gleichung hat man also einen Normaleneinheitsvektor
.
Für diese Gleichung hat man also einen Normaleneinheitsvektor 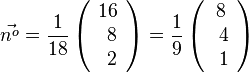 .
.
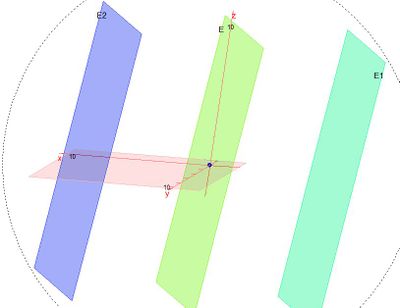
Zu einer zu E parallelen Ebene im Abstand 9 kommt man, wenn man neun mal diesen Normaleneinheitsvektor 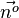 oder
oder 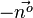 aneinandersetzt.
aneinandersetzt.
Deren HNF sind dann 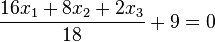 oder
oder 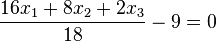 . (Berechnet man den Abstand des Ursprungs O (liegt in E) von diesen Ebenen kommt jeweils 9 heraus!)
. (Berechnet man den Abstand des Ursprungs O (liegt in E) von diesen Ebenen kommt jeweils 9 heraus!)
Schreibt man die Ebenengleichungen nur als Normalenform analog der Ebenengleichung für E, dann lauten sie 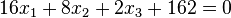 und
und 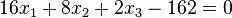 .
.
30px Merke
Bei gleichen Objekten (Gerade - Gerade) bzw. (Ebene - Ebene) wird cos zur Winkelberechnung verwendet. Bei ungleichen Objekten (Gerade - Ebene) wird sin zur Winkelberechnung verwendet. |
S. 154/6
a) Gleichsetzen der zwei Geradengleichungen liefert den Schnittpunkt (S(1;-1;0).
Für den Schnittwinkel interessieren nur die Richtungsvektoren der Geraden. Man erhält ihn aus 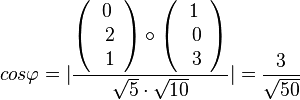 . Es ist
. Es ist 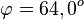 .
.
Ich lasse die Betragsstriche meist weg. Ist das Ergebnis für cos oder sin negativ, dann nimmt man einfach hier den Betrag
und erhält dann den spitzen Winkel.
b) S(0;2;-1) und 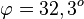
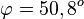
S. 154/7
a) Setzt man g in E ein, erhält man diese Gleichung 3(1+k) - (-2) - (-k) = 1 und k = -1. S(0;-2;1)
Für den Schnittwinkel interessieren der Richtungsvektor von g und der Normalenvektor der Ebene E. 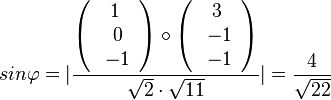 und
und 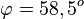
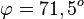
S. 154/8
a) Für den Schnittwinkel interessieren die zwei Normalenvektoren der Ebene. 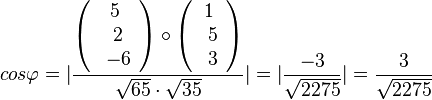 und
und 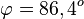
b) 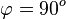
c) 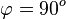
d) Hier ist es sinnvoll beide Ebenengleichungen in Normalenform zu schreiben;
E1: 5x1 - 6x2 - 2x3 + 3 = 0 und E2: 2x1 + x3 -3 = 0
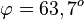
S. 154/9
a) Man hat die Gleichung 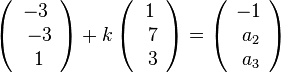
Aus der 1. Koordinatengleichung -3 + k = -1 folgt k = 2.
Für die 2. Koordinatengleichung ergibt sich -3 + 14 = a2, also a2=11.
Für die 3. Koordinatengleichung ergibt sich 1 + 6 = 3, also a3=7.
Also ist A(-1;11;7)
b) X ist ein Punkt auf g und hat dem Ortsvektor 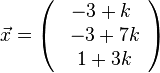 . Soll X Lotfusspunkt F des Lotes von P auf g sein, dann steht der Vektor
. Soll X Lotfusspunkt F des Lotes von P auf g sein, dann steht der Vektor 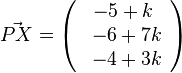 senkrecht auf dem Richtungsvektor
senkrecht auf dem Richtungsvektor  der Geraden. Also muss
der Geraden. Also muss 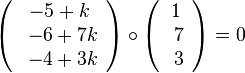 sein. Dies führt zur Gleichung
sein. Dies führt zur Gleichung
-5 + k + 7(-6 + 7k) + 3(-4+3k) = 0 und -59 + 59k = 0, also k = 1 und F(-2;4;4).
c) Den Spiegelpunkt A* von A bei Punktspiegelung am Zentrum Z = F(-2;4;4) erhält man durch 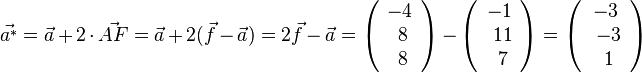 , also A*(-3;-3;1) .
, also A*(-3;-3;1) .
Analog erhält man P*(-6;5;3)
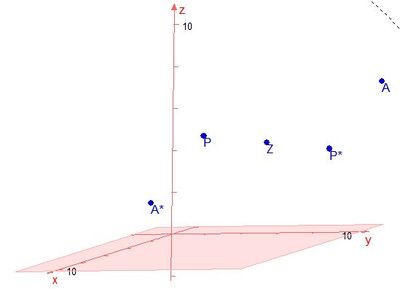
Den Flächeninhalt dieses Parallelogramms kann man nun berechnen.
elementar: Den Flächeninhalt eines Parallelogramms berechnet man mit der Formel A = g·h . Also muss man sich überlegen was ist g und was ist h. Die Punkte A, Z und A* liegen auf der Geraden g.
Man sieht, dass die beiden Dreiecke AA*P und AA*P* das Parallelogramm ergeben. Z = F ist der Lotfusspunkt des Lotes von P auf g, also ist die 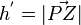 die Höhe des Dreiecks AA*P und
die Höhe des Dreiecks AA*P und 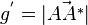 die Grundlinie des Dreiecks . Damit ergbit
die Grundlinie des Dreiecks . Damit ergbit