Aufgabe
Schaue dir zur Wiederholung das anfangs genannte Video
vollständig an.
a) Welche andere Bezeichnung gibt es für Amplitude?
b) Wodurch ist die Ruhelage ausgzeichnet?
c) Warum bewegt sich die Kugel bei einer Schwingung durch die Ruhelage?
d) Welche Aussage kannst du über die Beschleunigung der Kugel bei einer Federschwingung treffen?
Was bedeutet das für den Quotienten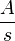 
?
Wie heißt eine solche Schwingung?
e) Benenne die Bewegungsgleichungen für eine harmonische Schwingung, wenn der Körper nach oben ausgelenkt und im oberen Umkehrpunkt losgelassen wird.
[Lösung anzeigen][Lösung ausblenden]
a) Scheitelwert
b) In der Ruhelage wirkt keine resultierende Kraft auf die Kugel.
Die Ruhelage ist die Lage in die der Körper bei einer gedämpften Schwingung zur Ruhe kommt.
c) Aufgrund ihrer Trägheit bewegt sich die Kugel im Verlauf einer Schwingung durch die Ruhelage weiter.
d) Bei einer Federschwingung ist die Beschleunigung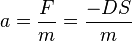 
Der Quotient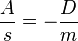 
ist konstant, da sich bei der Schwingung D und m nicht ändern. Also ist die Beschleunigung a direkt proportional zur Auslenkung s.
Eine solche Schwingung heißt harmonische Schwingung.
e) Fehler beim Parsen(Unbekannte Funktion „\oomega“): s(t) = s_0 \cdot cos(\oomega \cdot t)
, dabei ist s0 die Amplitude der Schwingung und Fehler beim Parsen(Syntaxfehler): }\omega = \frac{2\pi}{T}
die Winkelgeschwindigkeit und T die Schwingungsdauer. Zum Zeitpunkt t = 0s befindet sich der Pendelkörper im oberen Scheitelpunkt und wird dort losgelassen.
Fehler beim Parsen(Unbekannte Funktion „\oomega“): v(t) = - s_0 \cdot \omega \cdot sin(\oomega \cdot t)
Fehler beim Parsen(Unbekannte Funktion „\oomega“): a(t) = - s_0 \cdot \omega^2 \cdot cos(\oomega \cdot t)
