Aufgabe
Schaue dir zur Wiederholung das anfangs genannte Video
vollständig an.
a) Welche andere Bezeichnung gibt es für Amplitude?
b) Wodurch ist die Ruhelage ausgzeichnet?
c) Warum bewegt sich die Kugel bei einer Schwingung durch die Ruhelage?
d) Welche Aussage kannst du über die Beschleunigung der Kugel bei einer Federschwingung treffen?
Was bedeutet das für den Quotienten 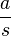 ?
?
Wie heißt eine solche Schwingung?
e) Benenne die Bewegungsgleichungen für eine harmonische Schwingung, wenn der Körper nach oben ausgelenkt und zur Zeit t = 0s im oberen Umkehrpunkt losgelassen wird.
Gib die Bewegungsgleichungen auch für den konkreten Fall einer Schwingung mit s0 = 0,1m und T = 2s an und zeichne ein ts-Diagramm.
f) Für eine harmonische Schwingung gilt ein besonderes Kraftgesetz. Benenne es und erkläre es am Beispiel des Federpendels.
[Lösung anzeigen][Lösung ausblenden]
Und nun noch ein paar Aufgaben aus dem Buch.
S. 91/3
[Lösung anzeigen][Lösung ausblenden]
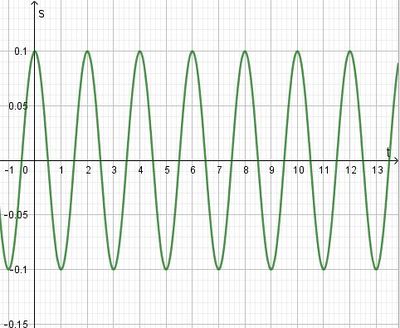
a9 in 1s gibt es 2,5 Schwingungen, also 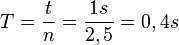 .
.
Die Frequenz f ist 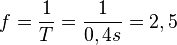 . (Das hat man ja eigentlich schon gerade aus dem Diagramm abgelesen.)
. (Das hat man ja eigentlich schon gerade aus dem Diagramm abgelesen.)
Die 100. Schwingung ist nach t = 100 ·0,4s = 40s erfolgt.
In einer Minute finden 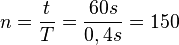 Schwingungen statt.
Schwingungen statt.
b)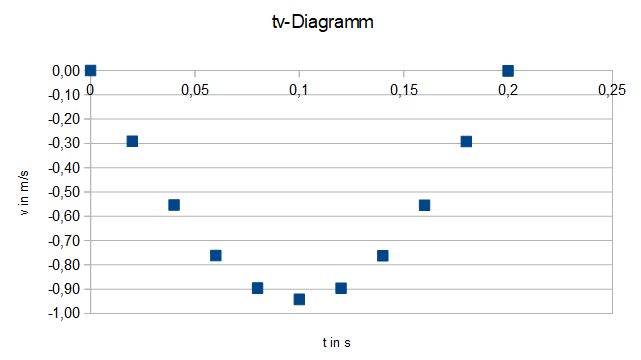
Das Wägestück ist am schnellsten, wenn es sich durch die Ruhelage bewegt.
Man kann es auch berechnen. Es ist 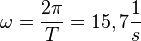 und
und 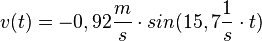
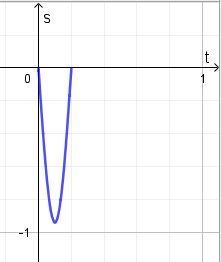
c) 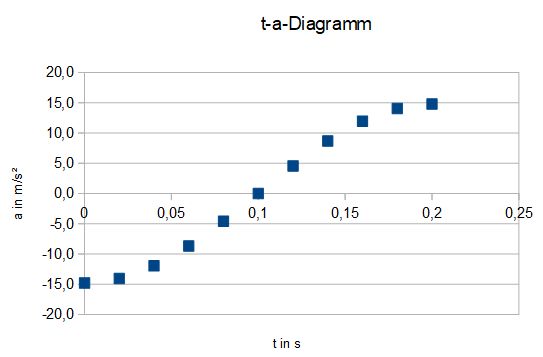
Es scheint das tx-Diagramm an der x-Achse gespiegelt zu sein. Es ist im ta-Diagramm ein -cos !
d)Das Wägestück hat die betragsmäßig größte Beschleunigungen in den Umkehrpunkten oben und unten.
Unten ist die Beschleunigung am größten, da sie dort positiv ist (sie geht nach oben in positive x-Richtung).
Die beschleunigende Kraft F unten ist F= m·a = 0,1kg ·15 m/s² = 1,5N und oben F = -1,5N.
e) Die Federkonstante D ist durch
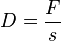
gegeben. Setzt man F = 1,5N und s = 0,06m ein ergibt sich
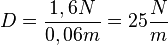
S. 92/2
[Lösung anzeigen][Lösung ausblenden]
F = D·s, also 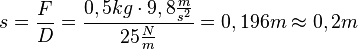
b) Die Beschleunigung ist beim Durchgang durch die Ruhelage 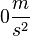 .
.
In den Umkehrpunkten ist die Beschleunigung
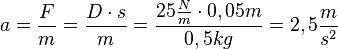
S. 92/3
{{Lösung versteckt|1=1° entspricht 0,017; 10° entspricht 0,175; 15° entspricht 0,262; 90° entspricht 1,57;
0,1 entspricht 5,7°; 0,5 entspricht 28,6°; 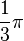 entspricht 60°;
entspricht 60°; 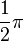 entspricht 90°.
entspricht 90°.
b) Es ist 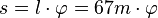 wobei der Winkel Fehler beim Parsen(Lexikalischer Fehler): \varphi</varphi> im Bogenmaß sein muss.<br> 1° entspricht 0,0175, also s = 67m ·0,0175 = 1,17m<br> 10° entspricht 0,175, also s = 67m · 0,175 = 11,7m<br> <math>s=\frac{1}{6} \pi \cdot 67m=35m}} S. 92/4 {{Lösung versteckt|1= }}
wobei der Winkel Fehler beim Parsen(Lexikalischer Fehler): \varphi</varphi> im Bogenmaß sein muss.<br> 1° entspricht 0,0175, also s = 67m ·0,0175 = 1,17m<br> 10° entspricht 0,175, also s = 67m · 0,175 = 11,7m<br> <math>s=\frac{1}{6} \pi \cdot 67m=35m}} S. 92/4 {{Lösung versteckt|1= }}
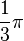 entspricht 60°;
entspricht 60°; 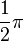 entspricht 90°.
entspricht 90°.
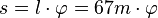 wobei der Winkel Fehler beim Parsen(Lexikalischer Fehler): \varphi</varphi> im Bogenmaß sein muss.<br> 1° entspricht 0,0175, also s = 67m ·0,0175 = 1,17m<br> 10° entspricht 0,175, also s = 67m · 0,175 = 11,7m<br> <math>s=\frac{1}{6} \pi \cdot 67m=35m}} S. 92/4 {{Lösung versteckt|1= }}
wobei der Winkel Fehler beim Parsen(Lexikalischer Fehler): \varphi</varphi> im Bogenmaß sein muss.<br> 1° entspricht 0,0175, also s = 67m ·0,0175 = 1,17m<br> 10° entspricht 0,175, also s = 67m · 0,175 = 11,7m<br> <math>s=\frac{1}{6} \pi \cdot 67m=35m}} S. 92/4 {{Lösung versteckt|1= }}
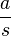 ?
?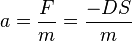
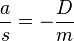 ist konstant, da sich bei der Schwingung D und m nicht ändern. Also ist die Beschleunigung a direkt proportional zur Auslenkung s.
ist konstant, da sich bei der Schwingung D und m nicht ändern. Also ist die Beschleunigung a direkt proportional zur Auslenkung s. 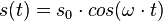 , dabei ist s0 die Amplitude der Schwingung und
, dabei ist s0 die Amplitude der Schwingung und 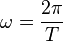 die Winkelgeschwindigkeit und T die Schwingungsdauer. Zum Zeitpunkt t = 0s befindet sich der Pendelkörper im oberen Scheitelpunkt und wird dort losgelassen.
die Winkelgeschwindigkeit und T die Schwingungsdauer. Zum Zeitpunkt t = 0s befindet sich der Pendelkörper im oberen Scheitelpunkt und wird dort losgelassen. 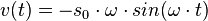
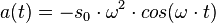
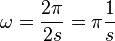 und
und 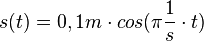
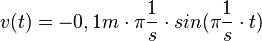
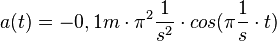
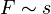
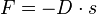 . D ist die Federkonstante, die für eine bestimmte Feder konstant ist. Also ist
. D ist die Federkonstante, die für eine bestimmte Feder konstant ist. Also ist 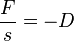 , was ein Kennzeichen einer direkten Proportionalität ist. Das Minuszeichen bei D bedeutet, dass die Richtung der Kraft F entgegengesetzt der Auslenkung s ist. Es handelt sich also um eine rücktreibende Kraft, die immer versucht den Körper wieder in die Ruhelage zu bringen.
, was ein Kennzeichen einer direkten Proportionalität ist. Das Minuszeichen bei D bedeutet, dass die Richtung der Kraft F entgegengesetzt der Auslenkung s ist. Es handelt sich also um eine rücktreibende Kraft, die immer versucht den Körper wieder in die Ruhelage zu bringen.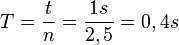 .
. 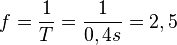 . (Das hat man ja eigentlich schon gerade aus dem Diagramm abgelesen.)
. (Das hat man ja eigentlich schon gerade aus dem Diagramm abgelesen.)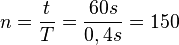 Schwingungen statt.
Schwingungen statt.

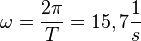 und
und 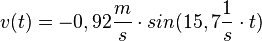


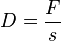 gegeben. Setzt man F = 1,5N und s = 0,06m ein ergibt sich
gegeben. Setzt man F = 1,5N und s = 0,06m ein ergibt sich 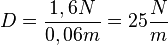
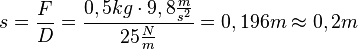
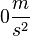 .
.