Abstands- und Winkelbestimmungen: Unterschied zwischen den Versionen
| Zeile 10: | Zeile 10: | ||
Für die Hessesche Normalform (HNF) muss außerdem gelten, dass <math>\vec{n} \circ \vec{a} > 0</math> ist. Das ist so festgelegt. In der HNF in Koordinatenschreibweise muss also vor der Konstanten <math>\vec{n} \circ \vec{a} > 0</math> ein Minuszeichen stehen! | Für die Hessesche Normalform (HNF) muss außerdem gelten, dass <math>\vec{n} \circ \vec{a} > 0</math> ist. Das ist so festgelegt. In der HNF in Koordinatenschreibweise muss also vor der Konstanten <math>\vec{n} \circ \vec{a} > 0</math> ein Minuszeichen stehen! | ||
| − | {{Aufgaben-blau||2= Geben Sie die Hessesche Normalenform an: <br> | + | {{Aufgaben-blau|1|2= Geben Sie die Hessesche Normalenform an: <br> |
| − | a) 2x<sub>1</sub>+ x<sub>2</sub> - 2x<sub>3</sub> - 4 = 0 | + | a) 2x<sub>1</sub>+ x<sub>2</sub> - 2x<sub>3</sub> - 4 = 0<br> |
b) 3x<sub>1</sub>+ x<sub>2</sub> - 20x<sub>3</sub> + 45 = 0 | b) 3x<sub>1</sub>+ x<sub>2</sub> - 20x<sub>3</sub> + 45 = 0 | ||
}} | }} | ||
| Zeile 19: | Zeile 19: | ||
}} | }} | ||
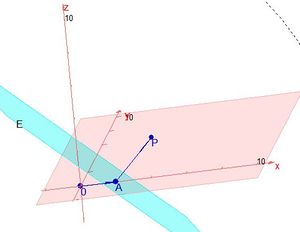
| − | {{Aufgaben-blau||2=Für die erste Ebene steht in der Normalenform -4, also ist das Skalarprodukt <math>\vec{n} \circ \vec{a} = 4</math>, positiv.<br> Betrachten Sie für diese Ebene den den Normalenvektor <math>\vec{n}</math> und den Vektor <math>\vec{a}</math> . Hier ist der Normalenvektor <math>\vec{n} = | + | {{Aufgaben-blau|2|2=Für die erste Ebene steht in der Normalenform -4, also ist das Skalarprodukt <math>\vec{n} \circ \vec{a} = 4</math>, positiv.<br> Betrachten Sie für diese Ebene den den Normalenvektor <math>\vec{n}</math> und den Vektor <math>\vec{a}</math> . Hier ist der Normalenvektor <math>\vec{n} = \vec{AP}</math> .<br> |
[[Datei:Hnf1.jpg|HNF_1|300px]]<br> | [[Datei:Hnf1.jpg|HNF_1|300px]]<br> | ||
Was stellen Sie fest? }} | Was stellen Sie fest? }} | ||
| − | {{Lösung versteckt| Man sieht, dass beide Vektoren vom Urprung aus in die gleiche durch die Ebene E | + | {{Lösung versteckt|Die Ebene E teilt den Raum in zwei Halbräume. Man sieht, dass beide Vektoren vom Urprung aus in die gleiche durch die Ebene E erzeugten Halbraum zeigen. <math>\vec{n}</math> und <math> \vec{a}</math> haben in etwa "die gleiche Richtung", das Skalarprodukt ist positiv.}} |
| − | Die Festlegung | + | |
| + | Die Festlegung <math>\vec{n} \circ \vec{a} > 0</math> bedeutet anschaulich, dass vom Ursprung aus die <math>\vec{n}</math> und <math> \vec{a}</math> haben in etwa "die gleiche Richtung" haben. | ||
| + | |||
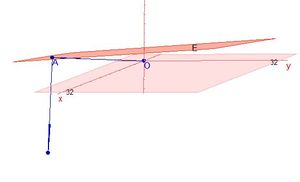
| + | {{Aufgaben-blau|3|2=Die Ebene 3x<sub>1</sub>+ x<sub>2</sub> - 20x<sub>3</sub> + 45 = 0 ist die Ebene E aus Aufgabe 147/16. Für diese Ebene stellt sich die Situation so dar. <br> | ||
| + | [[Datei:Hnf2.jpg|HNF_2|300px]]<br> | ||
| + | Was stellen Sie hier fest?}} | ||
| + | |||
| + | {{Lösung versteckt|1=Hier sieht man, dass die Vektoren <math>\vec{n}</math> und <math> \vec{a} </math> in verschiedene durch die Ebene E erzeugten Halbräume zeigen. Ihr Zwischenwinkel ist > 90°. Also ist ihr Skalarprodukt negativ und in der Normalenform steht -(-45) = 45. Dann muss man für die HNF das Vorzeichen ändern, indem man vor den Bruch ein Minuszeichen schreibt. dies ist in Aufgabe 1 erfolgt.}} | ||
| + | |||
| + | |||
| + | Normiert man den Normalenvektor <math>\vec{n}</math> und geht vom Lot | ||
Version vom 22. März 2020, 11:10 Uhr
Dieses Thema ist im Buch auf S. 151 ausführlich beschrieben. Lesen Sie bitte diese Seite aufmerksam.
Hintergrund zur Hesseschen Normalenform (HNF):
Wir kennen die Normalenform einer Ebenengleichung. 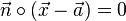 .
.
Normiert man den Normalenvektoer  , also
, also 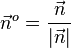 , dann erhält man einen Vektor
, dann erhält man einen Vektor 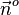 , der die gleiche Richtung wie der Normalenvektor
, der die gleiche Richtung wie der Normalenvektor  und die Länge
und die Länge 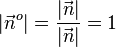 hat.
hat.
Mit dem Vektor 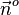 erstellt man ebenso eine Normalenform
erstellt man ebenso eine Normalenform 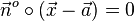 der Ebene. Man kann dies umformen und in Koordinatenschreibweise angeben:
der Ebene. Man kann dies umformen und in Koordinatenschreibweise angeben:
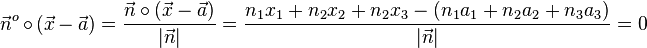
Für die Hessesche Normalform (HNF) muss außerdem gelten, dass 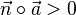 ist. Das ist so festgelegt. In der HNF in Koordinatenschreibweise muss also vor der Konstanten
ist. Das ist so festgelegt. In der HNF in Koordinatenschreibweise muss also vor der Konstanten 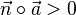 ein Minuszeichen stehen!
ein Minuszeichen stehen!
a) 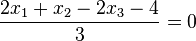
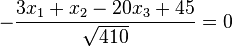 Beachten Sie das Minuszeichen vor dem Bruch. Man kann dieses Minuszeichen in den Zähler bringen und hat dann diese HNF
Beachten Sie das Minuszeichen vor dem Bruch. Man kann dieses Minuszeichen in den Zähler bringen und hat dann diese HNF 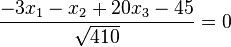
 und
und 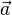 haben in etwa "die gleiche Richtung", das Skalarprodukt ist positiv.
haben in etwa "die gleiche Richtung", das Skalarprodukt ist positiv.
Die Festlegung 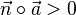 bedeutet anschaulich, dass vom Ursprung aus die
bedeutet anschaulich, dass vom Ursprung aus die  und
und 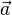 haben in etwa "die gleiche Richtung" haben.
haben in etwa "die gleiche Richtung" haben.
 und
und 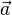 in verschiedene durch die Ebene E erzeugten Halbräume zeigen. Ihr Zwischenwinkel ist > 90°. Also ist ihr Skalarprodukt negativ und in der Normalenform steht -(-45) = 45. Dann muss man für die HNF das Vorzeichen ändern, indem man vor den Bruch ein Minuszeichen schreibt. dies ist in Aufgabe 1 erfolgt.
in verschiedene durch die Ebene E erzeugten Halbräume zeigen. Ihr Zwischenwinkel ist > 90°. Also ist ihr Skalarprodukt negativ und in der Normalenform steht -(-45) = 45. Dann muss man für die HNF das Vorzeichen ändern, indem man vor den Bruch ein Minuszeichen schreibt. dies ist in Aufgabe 1 erfolgt.
Normiert man den Normalenvektor  und geht vom Lot
und geht vom Lot
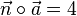 , positiv.
, positiv.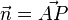 .
.