M10 Grenzwert und Exponentialfunktionen: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „=Exponentialfunktionen= {{Merksatz|MERK=Die Exponentialfunktion <math>f: x \rightarrow a^x</math> mit a > 0 gilt: 0 < a < 1: <math>\lim_{x \to -\infty} a^x =…“) |
|||
| Zeile 71: | Zeile 71: | ||
h) <math>f:x \rightarrow -2cos(x)</math> <br> | h) <math>f:x \rightarrow -2cos(x)</math> <br> | ||
Zum Überprüfen die Funktionsterme in GeoGebra eingeben! }} | Zum Überprüfen die Funktionsterme in GeoGebra eingeben! }} | ||
| + | |||
| + | {{Aufgaben-blau|3|2=Buch S. 127 / 9 }} | ||
| + | |||
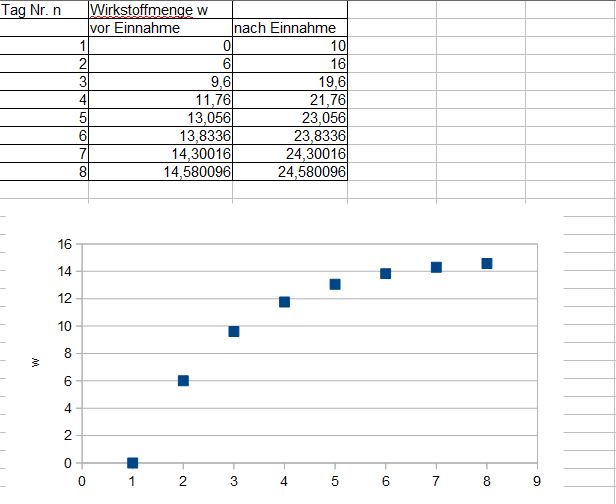
| + | {{Lösung versteckt|1=a,b)[[Datei:127-9a 1.jpg]] | ||
| + | |||
| + | c) Ansatz: <math>w_n=a-b\cdot 0,6^n</math>.<br> | ||
| + | Für n = 1 ist w<sub>1</sub> = 0, also I: <math>0 = a - b\cdot 0,6</math><br> | ||
| + | Für n = 2 ist w<sub>2</sub> = 6, also II: <math>6 = a - b \cdot 0,36</math><br> | ||
| + | II - I: 6 = 0,24b ergibt b = 25, a = 15<br> | ||
| + | <math>w_n=15-25\cdot 0,6^n</math><br> | ||
| + | [[Datei:127-9c.jpg]]<br> | ||
| + | Bei diesem Ansatz geht man von einem Sättigungswert a aus, der durch die regelmäßige Einnahme erreicht wird. | ||
| + | |||
| + | d) Aus dem Graphen der Funktion aus c) sieht man, dass der Wirkstoff im Körper sich dem Wert 15 annähert.<<br> | ||
| + | Setzt man die Tabelle aus a) fort<br> | ||
| + | [[Datei:127-9a 2.jpg]] <br> | ||
| + | so sieht man, dass w vor der Einnahme gegen 15 konvergiert. <br> | ||
| + | Die Wirkstoffmenge vor der Einnahme ist für <math>n \to \infty</math>: <math>\lim_{n \to \infty} = 15</math> Dies ist der Sättigungswert des Wirkstoffes im Körper, der sich auf lange Sicht einstellen wird. | ||
| + | |||
| + | e) <math>w_n=15-25\cdot 0,6^n</math> ist der Wirkstoff am Tag n vor der Einnahme. Nimmt man nun das Medikament ein, dann erhöht sich der Wert <math>w_n + 10</math> und wird im Verlauf der nächsten 24 Stunden um 40% reduziert. Es ist dann <math>w_{n+1}=(15-25\cdot 0,6^n+10)\cdot 0,6=(25 - 25\cdot 0,6^n)\cdot 0,6=15-25\cdot 0,6^n \cdot 0,6 =15 - 25\cdot 0,6^{n+1}</math> }} | ||
Version vom 14. Mai 2021, 17:19 Uhr
Exponentialfunktionen
|
Merke:
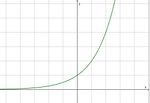
Die Exponentialfunktion |
124/2 Man weiß von Exponentialfunktionen 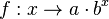 , dass
, dass 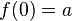 und
und 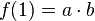 ist. Wenn a = 1 ist, dann ist
ist. Wenn a = 1 ist, dann ist 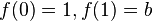 . Damit findet man leicht die Zuordnung Term - Graph.
. Damit findet man leicht die Zuordnung Term - Graph.
A - k
B - f
C - m
D - h
E - g
125/3a) 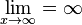 , die Funktion divergiert für
, die Funktion divergiert für 
b) Die Funktion konvergiert für  , es ist
, es ist 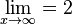 (?)
(?)
c) Die Funktion konvergiert für  , es ist
, es ist 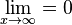
d) Die Funktion konvergiert für  , es ist
, es ist 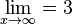 (?)
(?)
e) Die Funktion divergiert unbestimmt für 

126/6
a) 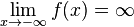 divergiert und
divergiert und 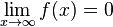 konvergiert
konvergiert
b) 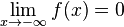 konvergiert und
konvergiert und 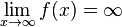 divergiert
divergiert
c) 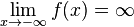 divergiert und
divergiert und 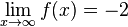 konvergiert
konvergiert
d) 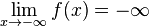 divergiert und
divergiert und 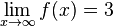 konvergiert
konvergiert
e) 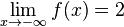 konvergiert und
konvergiert und 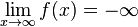 divergiert
divergiert
f) 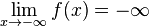 divergiert und
divergiert und 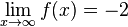 konvergiert
konvergiert
g) Die Funktion divergiert unbestimmt.
h) 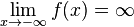 divergiert und
divergiert und 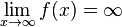 divergiert
divergiert
i) 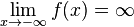 divergiert und
divergiert und 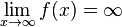 divergiert
divergiert
k) 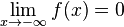 konvergiert und
konvergiert und 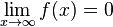 konvergiert
konvergiert
l) 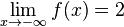 konvergiert und
konvergiert und 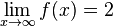 konvergiert
konvergiert
m) 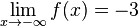 konvergiert und
konvergiert und 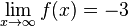 konvergiert
konvergiert
n) 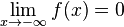 konvergiert und
konvergiert und 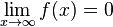 konvergiert
konvergiert
o) Die Funktion divergiert unbestimmt.
p) 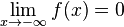 konvergiert und
konvergiert und 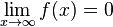 konvergiert
konvergiert
126/7
a) Ist möglich, da z.B. 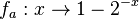 stets unter der Geraden y = 1 verläuft.
stets unter der Geraden y = 1 verläuft.
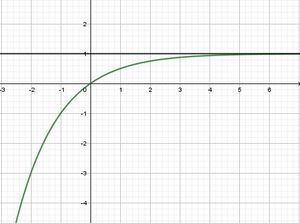
b) Ist möglich, da die Funktion 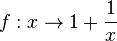 oberhalb und unterhalb der Geraden y = 1 verläuft.
oberhalb und unterhalb der Geraden y = 1 verläuft.
c) Ist falsch, denn wenn der Graph von f stets oberhalb der Gerade y = 1 verläuft und die Funktionswerte mit wachsenden x auch größer werden, dann kann der Grenzwert für  nicht 1 sein.
nicht 1 sein.
d) Ist möglich bei der Funktion 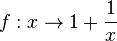 .
.
e) Ist möglich bei der Funktion 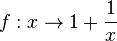 .
.
Muss aber nicht sein, es gibt auch Funktionen, deren Abstand zur Geraden y = 1 erst ab Werten x > 1000 kleiner als 1/100 ist. Z.B. ist für die Funktion 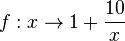 f(100)=1,1 und damit ist der Abstand zur Geraden 0,1 und f(1000)=1,01.
f(100)=1,1 und damit ist der Abstand zur Geraden 0,1 und f(1000)=1,01.
f) Der Term (-1)n nimmt für n = 1, 2, 3, 4, ... die Werte -1, 1, -1, 1, .... an. Die Funktionswerte alternieren stets und der Grenzwert ist nicht bestimmt. Also ist die Aussage falsch.
g) Diese Funktionswerte nähern sich mit wachsendem n immer mehr der Zahl 1 an, obwohl sie auch hier stets wechselndes Vorzeichen haben.

126/8
a) 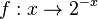
b) 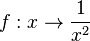
c) 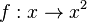
d) 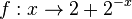
e) 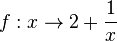
f) 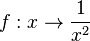
g) 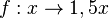
h) 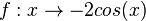
c) Ansatz: 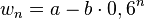 .
.
Für n = 1 ist w1 = 0, also I: 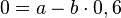
Für n = 2 ist w2 = 6, also II: 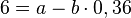
II - I: 6 = 0,24b ergibt b = 25, a = 15
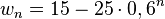
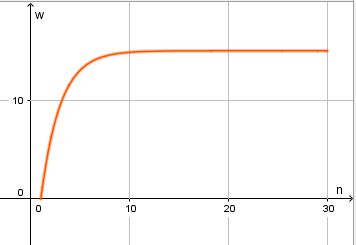
Bei diesem Ansatz geht man von einem Sättigungswert a aus, der durch die regelmäßige Einnahme erreicht wird.
d) Aus dem Graphen der Funktion aus c) sieht man, dass der Wirkstoff im Körper sich dem Wert 15 annähert.<
Setzt man die Tabelle aus a) fort
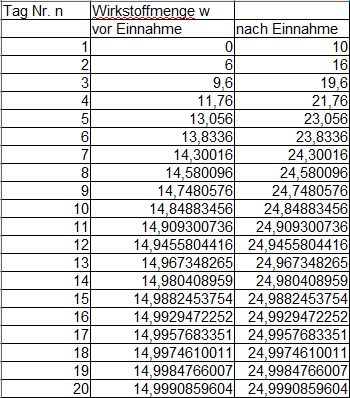
so sieht man, dass w vor der Einnahme gegen 15 konvergiert.
Die Wirkstoffmenge vor der Einnahme ist für 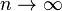 :
: 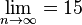 Dies ist der Sättigungswert des Wirkstoffes im Körper, der sich auf lange Sicht einstellen wird.
Dies ist der Sättigungswert des Wirkstoffes im Körper, der sich auf lange Sicht einstellen wird.
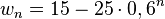 ist der Wirkstoff am Tag n vor der Einnahme. Nimmt man nun das Medikament ein, dann erhöht sich der Wert
ist der Wirkstoff am Tag n vor der Einnahme. Nimmt man nun das Medikament ein, dann erhöht sich der Wert 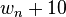 und wird im Verlauf der nächsten 24 Stunden um 40% reduziert. Es ist dann
und wird im Verlauf der nächsten 24 Stunden um 40% reduziert. Es ist dann 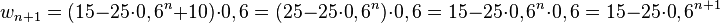

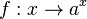 mit a > 0 gilt:
mit a > 0 gilt:
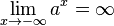 und
und 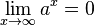

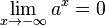 und
und 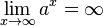
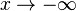 .
.