M11 Ableitung der Logarithmusfunktionen
Aus RSG-Wiki
Version vom 19. März 2021, 15:28 Uhr von Karlhaberl (Diskussion | Beiträge)
Die Ableitung der ln-Funktion erhält man aus der Tatsache, dass die ln-Funktion Umkehrfunktion zur e-Funktion ist. Für 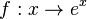 ist
ist 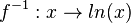 die Umkehrfunktion. Damit ist
die Umkehrfunktion. Damit ist 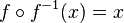 . Für die Ableitung gilt hier (
. Für die Ableitung gilt hier (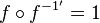 und mittels der Kettenregel erhält man
und mittels der Kettenregel erhält man
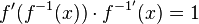 . Dies führt wieder zur Formel für die Ableitung der Umkehrfunktion
. Dies führt wieder zur Formel für die Ableitung der Umkehrfunktion 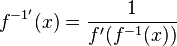 .
.
Die Ableitung der e-Funktion ist 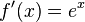 .
.
Damit erhält man für die Umkehrfunktion 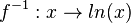 als Ableitung:
als Ableitung:
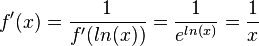 .
.
Also ist die Ableitung der natürlichen Logarithmusfunktion 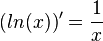 .
.
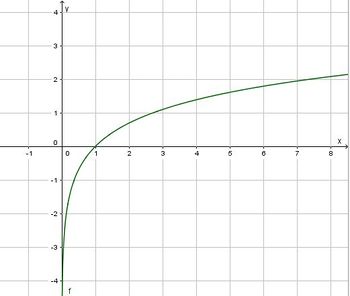
Im folgenden Applet kann man diese Aussage über die Ableitung der natürlichen Logarithmusfunktion  verifizieren. Über dem x-Wert des Punktes auf dem Graphen der ln-Funktion wird die Steigung der Tangente in dem Punkt an den Graphen angetragen. Dieser Punkt liegt auf der Hypberbel
verifizieren. Über dem x-Wert des Punktes auf dem Graphen der ln-Funktion wird die Steigung der Tangente in dem Punkt an den Graphen angetragen. Dieser Punkt liegt auf der Hypberbel  .
.
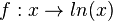 hat folgende Eigenschaften:
hat folgende Eigenschaften: