M11 Verknüpfte Ereignisse
|
Merke:
Der Ergebnisraum Das Ereignis E enthält alle für E günstigen Ergebnisse. Die einelementigen Ereignisse Ein Ereignis, das alle Ergebnisse des Zufallsexperiments enthält heißt sicheres Ereignis. Ein Ereignis, das bei dem Zufallsexperiment nicht eintreten kann, das also kein Ergebnis enthält ist ein unmögliches Ereignis. Das Ereignis |
| Sprechweisen | Schreibweisen |
|---|---|
| Gegenereignis zu A, Nicht A | 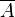 |
| Ereignis A und Ereignis B, Beide Ereinisse | 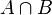 |
| Ereignis A oder Ereignis B | 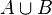 |
| Keines der beiden Ereignisse, Weder A noch B | 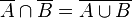 |
| Höchstens eines der beiden Ereignisse, Nicht beide Ereignisse | 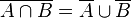 |
| Genau eines der beiden Ereignisse, Entweder A oder B | 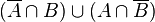 |
Im Buch auf S. 177 finden Sie zu den verknüpften Ereignissen schöne Veranschaulichungen.
178/1
a) 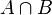
b) 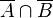
c) 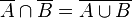
d) 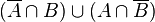
179/2 P(mindestens ein Würfel hat gerade Augenzahl)= 1 - P(kein Würfel hat gerade Augenzahl) = 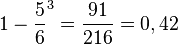
179/3
a) 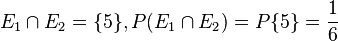
b) 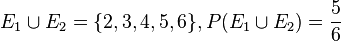
c) 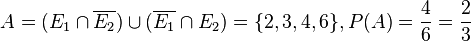
d) 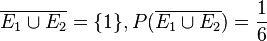
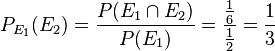

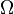 ist die Menge aller möglichen Ergebnisse. Es ist
ist die Menge aller möglichen Ergebnisse. Es ist 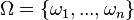 .
.
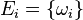 heißen Elementarereignisse.
heißen Elementarereignisse.
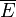 enthält alle für E ungünstigen Ergebnisse, also alle Ergebnisse, die nicht in E sind und heißt Gegenereignis von E.
enthält alle für E ungünstigen Ergebnisse, also alle Ergebnisse, die nicht in E sind und heißt Gegenereignis von E.

