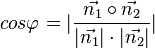Winkelberechnungen: Unterschied zwischen den Versionen
Aus RSG-Wiki
(Die Seite wurde neu angelegt: „{{Merksatz|MERK=Der (spitze oder rechte) Schnittwinkel <math>\varphi</math> zweier Geraden <math>g: \vec{x} = \vec{a} + r \vec{u}</math> und <math>h: \vec{x} =…“) |
|||
| Zeile 1: | Zeile 1: | ||
| + | Da dies im Buch auf S. 151 sehr schön dargestellt ist uns es nur um eine Anwendung des Skalarprodukts geht, sind nur die Ergebnisse notiert. | ||
| + | |||
{{Merksatz|MERK=Der (spitze oder rechte) Schnittwinkel <math>\varphi</math> zweier Geraden <math>g: \vec{x} = \vec{a} + r \vec{u}</math> und <math>h: \vec{x} = \vec{b} + r \vec{v}</math> ist gegeben durch <math> cos\varphi=\vert \frac{\vec{u}\circ\vec{v}}{\vert\vec{u}\vert\cdot\vert\vec{v}\vert}\vert</math>}} | {{Merksatz|MERK=Der (spitze oder rechte) Schnittwinkel <math>\varphi</math> zweier Geraden <math>g: \vec{x} = \vec{a} + r \vec{u}</math> und <math>h: \vec{x} = \vec{b} + r \vec{v}</math> ist gegeben durch <math> cos\varphi=\vert \frac{\vec{u}\circ\vec{v}}{\vert\vec{u}\vert\cdot\vert\vec{v}\vert}\vert</math>}} | ||
| Zeile 14: | Zeile 16: | ||
| + | {{Merke|1=Bei gleichen Objekten (Gerade - Gerade) bzw. (Ebene - Ebene) wird '''cos''' zur Winkelberechnung verwendet. | ||
| + | |||
| + | Bei ungleichen Objekten (Gerade - Ebene) wird '''sin''' zur Winkelberechnung verwendet.}} | ||
--------------------------------------------------------- | --------------------------------------------------------- | ||
| − | Zurück zu Abstands-_und_Winkelbestimmungen | + | Zurück zu [[Abstands-_und_Winkelbestimmungen]] |
Aktuelle Version vom 22. März 2020, 13:38 Uhr
Da dies im Buch auf S. 151 sehr schön dargestellt ist uns es nur um eine Anwendung des Skalarprodukts geht, sind nur die Ergebnisse notiert.
|
Merke:
Der (spitze oder rechte) Schnittwinkel |
|
Merke:
Der (spitze oder rechte) Schnittwinkel |
|
Merke:
Der (spitze oder rechte) Schnittwinkel |
|
Bei gleichen Objekten (Gerade - Gerade) bzw. (Ebene - Ebene) wird cos zur Winkelberechnung verwendet. Bei ungleichen Objekten (Gerade - Ebene) wird sin zur Winkelberechnung verwendet. |
Zurück zu Abstands-_und_Winkelbestimmungen

 zweier Geraden
zweier Geraden 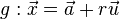 und
und 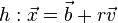 ist gegeben durch
ist gegeben durch 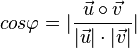
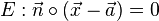 ist gegeben durch
ist gegeben durch 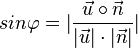
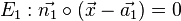 und einer Ebene
und einer Ebene 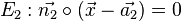 ist gegeben durch
ist gegeben durch