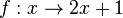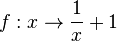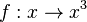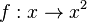Umkehrfunktion Beispiele: Unterschied zwischen den Versionen
| (Eine dazwischenliegende Version von einem Benutzer wird nicht angezeigt) | |||
| Zeile 6: | Zeile 6: | ||
Um das bisher behandelte zu üben beginnen wir mit ähnlichen Beispielen, also linearen Funktionen | Um das bisher behandelte zu üben beginnen wir mit ähnlichen Beispielen, also linearen Funktionen | ||
| − | {{ | + | {{Aufgaben-blau|1|2=Bestimme die Umkehrfunktion graphisch und rechnerisch der Funktion |
| − | Bestimme die Umkehrfunktion graphisch und rechnerisch der Funktion | + | |
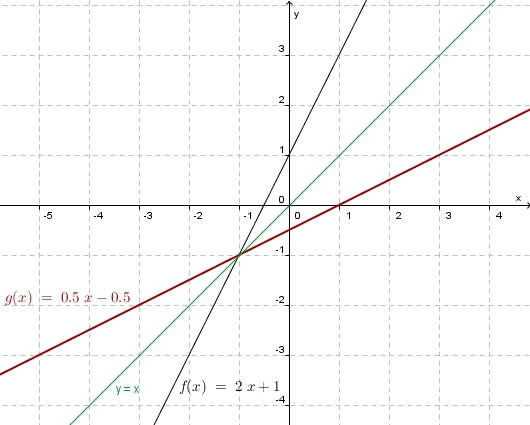
a) <math>f: x \rightarrow 2x + 1</math> | a) <math>f: x \rightarrow 2x + 1</math> | ||
| Zeile 30: | Zeile 29: | ||
Nun wollen wir auch andere Funktionstypen untersuchen: | Nun wollen wir auch andere Funktionstypen untersuchen: | ||
| − | {{ | + | {{Aufgaben-blau|2|2=Bestimme die Umkehrfunktion graphisch und algebraisch der Funktion |
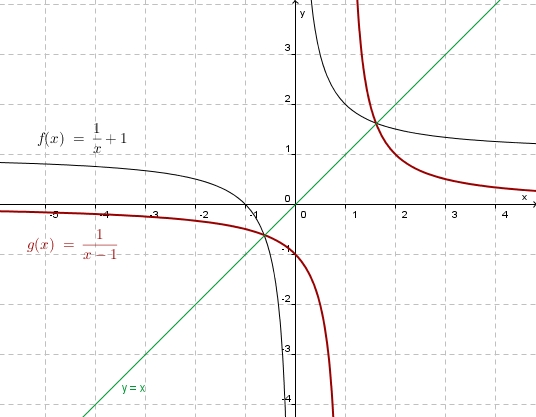
a) <math>f: x \rightarrow \frac{1}{x}+1</math> | a) <math>f: x \rightarrow \frac{1}{x}+1</math> | ||
| Zeile 56: | Zeile 55: | ||
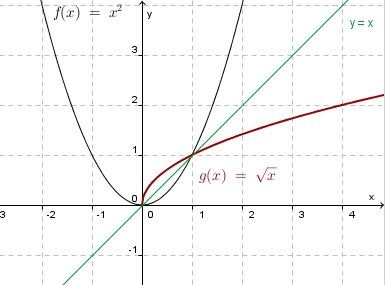
'''Rechnerisch: ''' <math> y =x^2</math><br> | '''Rechnerisch: ''' <math> y =x^2</math><br> | ||
x und y vertauschen: <math>x = y^2 </math><br> | x und y vertauschen: <math>x = y^2 </math><br> | ||
| − | nach y auflösen: <math>y = sqrt{x}</math> | + | nach y auflösen: <math>y = \sqrt{x}</math> |
}} | }} | ||
Aktuelle Version vom 23. April 2021, 09:52 Uhr
Startseite - Wertetabelle - Graph - Term - Beispiele - Definitions- und Wertemenge - Monotoniekriterium
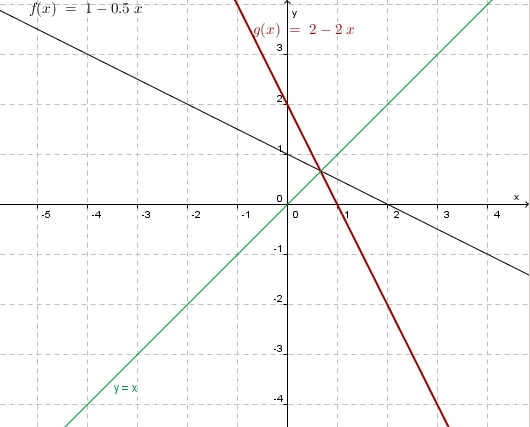
Um das bisher behandelte zu üben beginnen wir mit ähnlichen Beispielen, also linearen Funktionen
Rechnerisch: 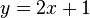
x und y vertauschen: 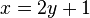
nach y auflösen: 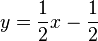
Rechnerisch: 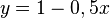
x und y vertauschen: 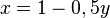
nach y auflösen: 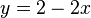
Nun wollen wir auch andere Funktionstypen untersuchen:
Rechnerisch: 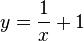
x und y vertauschen: 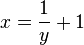
nach y auflösen: 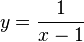
Rechnerisch: 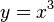
x und y vertauschen: 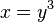
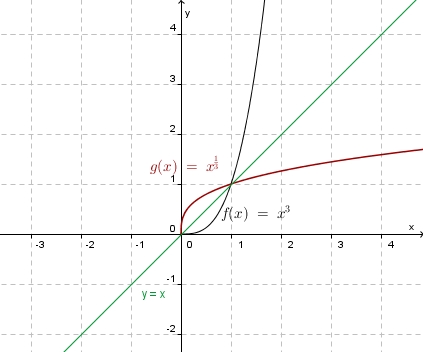
nach y auflösen: ![y = \sqrt[3]{x}](/images/math/3/0/5/3055a95564f016c3cb7958550ce93ffc.png)
Rechnerisch: 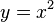
x und y vertauschen: 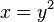
nach y auflösen: 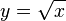
Bei den letzten Aufgabe hat man ein Problem. Bei der graphischen Lösung geht man von einem Punkt der 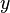 -Achse waagrecht zum Funktionsgraph der Funktion
-Achse waagrecht zum Funktionsgraph der Funktion  und von dort senkrecht zur
und von dort senkrecht zur 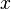 -Achse. Nur wie soll man von
-Achse. Nur wie soll man von 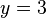 waagrecht losgehen? Nach links oder nach rechts?
waagrecht losgehen? Nach links oder nach rechts?
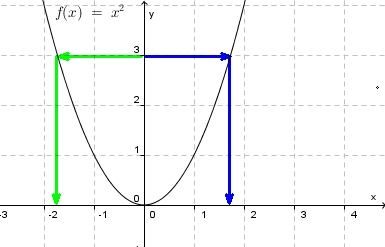
Dies wollen wir bei Definitions- und Wertemenge näher behandeln.
Zurück zur Startseite - Wertetabelle - Graph - Term - Beispiele - Definitions- und Wertemenge - Monotoniekriterium