Umkehrfunktion Term: Unterschied zwischen den Versionen
| Zeile 1: | Zeile 1: | ||
[[Die_Umkehrfunktion|Startseite]] - [[Umkehrfunktion_Wertetabelle|Wertetabelle]] - [[Umkehrfunktion_Graph|Graph]] - | [[Die_Umkehrfunktion|Startseite]] - [[Umkehrfunktion_Wertetabelle|Wertetabelle]] - [[Umkehrfunktion_Graph|Graph]] - | ||
| − | [[Umkehrfunktion_Term|Term]] - [[Umkehrfunktion_Beispiele|Beispiele]] - [[Umkehrfunktion_Definitions-_und_Wertemenge|Definitions- und Wertemenge]] - [[ | + | [[Umkehrfunktion_Term|Term]] - [[Umkehrfunktion_Beispiele|Beispiele]] - [[Umkehrfunktion_Definitions-_und_Wertemenge|Definitions- und Wertemenge]] - [[Umkehrfunktion_Monotonie|Monotoniekriterium]] |
---- | ---- | ||
| Zeile 29: | Zeile 29: | ||
Damit erhältst du die Gleichung der Umkehrfunktion. Da diese Funktion sehr eng mit der Funktion <math>f</math> zusammenhängt, schreibt man meist <math> f^{-1}</math> für sie. Damit ist zur Funktion <math>f : x \rightarrow 2x -1</math> die Umkehrfunktion <math>f^{-1}: x \rightarrow \frac{1}{2}x + \frac{1}{2}</math>. | Damit erhältst du die Gleichung der Umkehrfunktion. Da diese Funktion sehr eng mit der Funktion <math>f</math> zusammenhängt, schreibt man meist <math> f^{-1}</math> für sie. Damit ist zur Funktion <math>f : x \rightarrow 2x -1</math> die Umkehrfunktion <math>f^{-1}: x \rightarrow \frac{1}{2}x + \frac{1}{2}</math>. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ---- | ||
| + | Zurück zur [[Die_Umkehrfunktion|Startseite]] - [[Umkehrfunktion_Wertetabelle|Wertetabelle]] - [[Umkehrfunktion_Graph|Graph]] - [[Umkehrfunktion_Term|Term]] - [[Umkehrfunktion_Beispiele|Beispiele]] - [[Umkehrfunktion_Definitions-_und_Wertemenge|Definitions- und Wertemenge]] - [[Umkehrfunktion_Monotonie|Monotoniekriterium]] | ||
Version vom 23. Mai 2012, 19:03 Uhr
Startseite - Wertetabelle - Graph - Term - Beispiele - Definitions- und Wertemenge - Monotoniekriterium
Beim Graph hast du gesehen, dass beim Bilden des Graphen der Umkehrfunktion wieder eine Gerade entsteht. Aus dem Diagramm kannst du die Geradengleichung ablesen.
30px Aufgabe
1. Wie vertauscht man x- und y- Achse im Term? 2. Löse die Gleichung |
1. Man vertauscht im Term x und y.
2.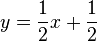
30px Merke
So findest du den Term der Umkehrfunktion:
2. Vertausche x und y
3. Löse nach y auf
|
Damit erhältst du die Gleichung der Umkehrfunktion. Da diese Funktion sehr eng mit der Funktion  zusammenhängt, schreibt man meist
zusammenhängt, schreibt man meist 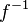 für sie. Damit ist zur Funktion
für sie. Damit ist zur Funktion 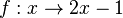 die Umkehrfunktion
die Umkehrfunktion 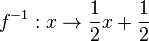 .
.
Zurück zur Startseite - Wertetabelle - Graph - Term - Beispiele - Definitions- und Wertemenge - Monotoniekriterium
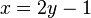 nach y auf.
nach y auf.