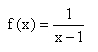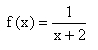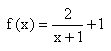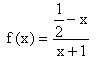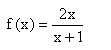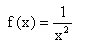M8 - Tests zu gebrochen-rationalen Funktionen: Unterschied zwischen den Versionen

Aus RSG-Wiki
Wechseln zu: Navigation, Suche
Zeile 52: Zeile 52:
 
{{Lösung versteckt|1=a) <math>f(x) = \frac{x}{x-1}</math> hat bei x = 1 eine Definitionslücke, D = Q\{1} und bei x = 0 eine Nullstelle.<br>
 
{{Lösung versteckt|1=a) <math>f(x) = \frac{x}{x-1}</math> hat bei x = 1 eine Definitionslücke, D = Q\{1} und bei x = 0 eine Nullstelle.<br>
 
b) <math>f(x) = \frac{x-2}{x+1}</math> hat bei x = -1 eine Definitionslücke und D = Q\{-1}; Nullstelle bei x = 2.<br>
 
b) <math>f(x) = \frac{x-2}{x+1}</math> hat bei x = -1 eine Definitionslücke und D = Q\{-1}; Nullstelle bei x = 2.<br>
−
c) f mit <math>f(x) = \frac{x+2}{x^2+1}</math> hat keine Definitionslücke, D = Q; Nullstelle bei x = -2<br>
+
c) f mit <math>f(x) = \frac{x+2}{x^2+1}</math> hat keine Definitionslücke (x<sup>2</sup> + 1 > 0), D = Q; Nullstelle bei x = -2<br>
 
d) <math>f(x) = \frac{x^2}{x^2-1}</math> hat wegen x<sup>2</sup>-1=(x+1)(x-1) zwei Definitionslücken x = -1 und x = 1, also D = Q\{-1;1} und Nullstelle bei x = 0.<br>
 
d) <math>f(x) = \frac{x^2}{x^2-1}</math> hat wegen x<sup>2</sup>-1=(x+1)(x-1) zwei Definitionslücken x = -1 und x = 1, also D = Q\{-1;1} und Nullstelle bei x = 0.<br>
 
e) <math>f(x) = \frac{2x+1}{x-5}</math> hat bei x = 5 eine Definitionslücke, D = Q\{5} und Nullstelle bei x = - 0,5.<br>
 
e) <math>f(x) = \frac{2x+1}{x-5}</math> hat bei x = 5 eine Definitionslücke, D = Q\{5} und Nullstelle bei x = - 0,5.<br>
Zeile 59: Zeile 59:
 
  Beachte: Ein Produkt hat den Wert 0, wenn ein Faktor den Wert 0 hat!
 
  Beachte: Ein Produkt hat den Wert 0, wenn ein Faktor den Wert 0 hat!
 
}}
 
}}
 +
 +
 +
Für die folgenden Tests, in denen Graphen und Funktionsterme gegeben sind, ist es hilfreich sich den Term anzusehen und zu überlegen wo Definitionslücken und Nullstellen auftreten. <br>
 +
Bei einer Definitionslücke hat man oftmals eine senkrechte Asymptote. <br>
 +
Bei der Nullstelle schneidet der Graph die x-Achse. <br>
 +
Waagrechte Asymptoten hat man, wenn <math>x \rightarrow -\infty</math> oder <math>x \rightarrow -\infty</math> geht. <br>
 +
 +
'''Test 1'''
 +
 +
Ordne den Funktionsgraphen den richtigen Term zu.
 +
<div class="lueckentext-quiz">
 +
{|
 +
|-
 +
| [[Bild:kh-rf-graph-1.jpg|150px]] || [[Bild:kh-rf-graph-2.jpg|150px]] || [[Bild:kh-rf-graph-3.jpg|150px]] || [[Bild:kh-rf-graph-4.jpg|150px]] || [[Bild:kh-rf-graph-5.jpg|150px]]  || [[Bild:kh-rf-graph-10.jpg|150px]]
 +
|-
 +
| <strong>  [[Bild:kh-rf-term-1.jpg]]  </strong>  || <strong> [[Bild:kh-rf-term-2.jpg]]  </strong> || <strong>  [[Bild:kh-rf-term-3.jpg]]  </strong> || <strong> [[Bild:kh-rf-term-4.jpg]]  </strong> || <strong> [[Bild:kh-rf-term-5.jpg]] </strong> || <strong> [[Bild:kh-rf-term-10.jpg]] </strong>
 +
|}
 +
</div>
 +
 +
'''Test 2'''
 +
 +
<div class="lueckentext-quiz">
 +
{|
 +
|-
 +
| [[Bild:kh-rf-term-1.jpg|150px]] || [[Bild:kh-rf-term-2.jpg|150px]] || [[Bild:kh-rf-term-3.jpg|150px]] || [[Bild:kh-rf-term-9.jpg|150px]] || [[Bild:kh-rf-term-5.jpg|150px]] 
 +
|-
 +
| <strong>  [[Bild:kh-rf-graph-1.jpg|150px]]  </strong>  || <strong> [[Bild:kh-rf-graph-2.jpg|150px]]  </strong> || <strong>  [[Bild:kh-rf-graph-3.jpg|150px]]  </strong> || <strong> [[Bild:kh-rf-graph-9.jpg|150px]]  </strong> || <strong> [[Bild:kh-rf-graph-5.jpg|150px]]  </strong>
 +
|}
 +
</div>
 +
 +
 +
 +
 +
 +
 +
Bearbeite folgende Übungen:
 +
 +
Halte beim Anklicken die Shift-Taste gedrückt, dann öffnet sich der Link in einem neuen Fenster!
 +
 +
{{Aufgaben-M|1|[[Rationale_Funktionen/Test1|Ordne den richtigen Term den gezeigten Graphen zu.]]}}
 +
 +
{{Aufgaben-M|2|[[Rationale_Funktionen/Test2|Ordne den richtigen Graph und angegebenen Termen zu.]]}}
 +
 +
{{Aufgaben-M|3|[[Rationale_Funktionen/Test3|Gib zu den Graphen bzw. Termen die richtige Definitionsmenge an.]]
 +
}}
 +
 +
{{Aufgaben-M|4|[[Rationale_Funktionen/Test4|Gib zu den Graphen bzw. Termen die Asymptoten an.]]]}}
 +
 +
{{Aufgaben-M|5|[[Rationale_Funktionen/Test5|Memory-Quiz]]}}
 +
 +
{{Aufgaben-M|6|[[Rationale_Funktionen/Test6|Knobel-Aufgaben]]}}

Version vom 28. März 2020, 11:43 Uhr

Auf dieser Seite kommen noch ein paar Tests, mit denen du schauen kannst wie sicher du im Umgang mit gebrochen-rationalen Funktionen bist.

Zuerst zur Wiederholung:

30px   Merke

Die Funktion f hat in x0 eine Nullstelle, wenn f(x0) = 0 ist.

Das hast du bei linearen Funktionen schon kennengelernt.


30px   Aufgabe

Bestimme die Nullstellen der linearen Funktionen f mit
a) f(x) = x - 1
b) f(x) = 2x + 1
c) f(x) = 5x
d) f(x) = 12x - 48
e) f(x) = -2x + 10
f) f(x) = 4 - 0,5x
g) f(x) = -2x -0,25
h) Welche Bedeutung haben die Nullstellen beim Graphen der Funktion?

a) x = 1
b) x = - 0,5
c) x = 0
d) x = 4
e) x = 5
f) x = 8
g) x = -0,125

h) Die Nullstellen der Funktion geben beim Graphen den Schnittpunkt mit der x-Achse (y=0) an.


Auch für gebrochen-rationale Funktionen kann man falls es Nullstellen gibt diese angeben.

30px   Merke

Ein Bruch ist 0, wenn der Zähler 0 ist.

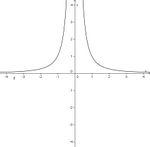
Beispiel: 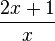\frac{2x+1}{x} hat den Wert 0, wenn der Zähler 2x+1 = 0 ist, also für x = -0,5.

Maehnrot.jpg
Merke:

Eine gebrochenrationale Funktion besitzt überall dort eine Nullstelle, wo der Zähler den Wert Null annimmt (und der Nenner jedoch ungleich Null ist).

Nimmt der Zähler einer gebrochen-rationalen Funktion für x0 den Wert 0 an und hat auch der Nenner für x0 den Wert 0, dann ist xo eine Definitionslücke und man darf x0 gar nicht einsetzen. Deshalb ist in dem Merksatz nur in Klammern angemerkt, dass der Nenner bei einer Nullstelle einen Wert ungleich 0 hat.


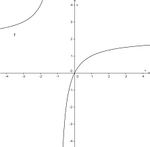
30px   A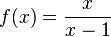ufgabe

Bestimme für die gebrochen-rationale Funktion f zuerst die Definitonslücke und Definitionsmenge und dann die Nullstelle(n)
a) f mit f(x) = \frac{x}{x-1}
b) f mit f(x) = \frac{x-2}{x+1}
c) f mit f(x) = \frac{x+2}{x^2+1}
d) f mit f(x) = \frac{x^2}{x^2-1}
e) f mit f(x) = \frac{2x+1}{x-5}
f) f mit f(x) = \frac{3-x}{x-3}
g) f mit f(x) = \frac{(x+1)(x-2)}{x-1}

a) f(x) = \frac{x}{x-1} hat bei x = 1 eine Definitionslücke, D = Q\{1} und bei x = 0 eine Nullstelle.
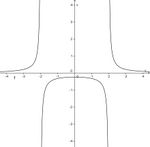
b) 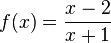f(x) = \frac{x-2}{x+1} hat bei x = -1 eine Definitionslücke und D = Q\{-1}; Nullstelle bei x = 2.
c) f mit 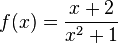f(x) = \frac{x+2}{x^2+1} hat keine Definitionslücke (x2 + 1 > 0), D = Q; Nullstelle bei x = -2
d) 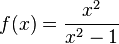f(x) = \frac{x^2}{x^2-1} hat wegen x2-1=(x+1)(x-1) zwei Definitionslücken x = -1 und x = 1, also D = Q\{-1;1} und Nullstelle bei x = 0.
e) 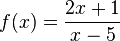f(x) = \frac{2x+1}{x-5} hat bei x = 5 eine Definitionslücke, D = Q\{5} und Nullstelle bei x = - 0,5.
f) f mit 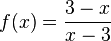f(x) = \frac{3-x}{x-3} hat bei x = 3 eine Definitionslücke, D = Q\{3}. Der Zähler nimmt für x = 3 den Wert 0 an, aber man darf die Definitionslücke ja gar nicht einsetzen, also ist 3 keine Nullstelle!
g) 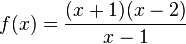f(x) = \frac{(x+1)(x-2)}{x-1} hat bei x = 1 eine Definitionslücke, D=Q\{1] und bei x = -1 und x = 2 Nullstellen.

Beachte: Ein Produkt hat den Wert 0, wenn ein Faktor den Wert 0 hat!


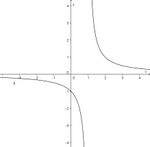
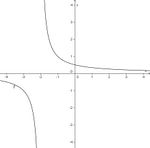
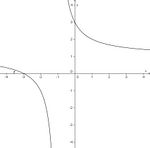
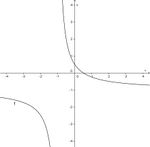
Für die folgenden Tests, in denen Graphen und Funktionsterme gegeben sind, ist es hilfreich sich den Term anzusehen und zu überlegen wo Definitionslücken und Nullstellen auftreten.
Bei einer Definitionslücke hat man oftmals eine senkrechte Asymptote.
Bei der Nullstelle schneidet der Graph die x-Achse.
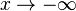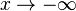Waagrechte Asymptoten hat man, wenn x \rightarrow -\infty oder x \rightarrow -\infty geht.

Test 1

Ordne den Funktionsgraphen den richtigen Term zu.

Kh-rf-graph-1.jpg Kh-rf-graph-2.jpg Kh-rf-graph-3.jpg Kh-rf-graph-4.jpg Kh-rf-graph-5.jpg Kh-rf-graph-10.jpg
Kh-rf-term-1.jpg Kh-rf-term-2.jpg Kh-rf-term-3.jpg Kh-rf-term-4.jpg Kh-rf-term-5.jpg Kh-rf-term-10.jpg

Test 2

Kh-rf-term-1.jpg Kh-rf-term-2.jpg Kh-rf-term-3.jpg Kh-rf-term-9.jpg Kh-rf-term-5.jpg
Kh-rf-graph-1.jpg Kh-rf-graph-2.jpg Kh-rf-graph-3.jpg Kh-rf-graph-9.jpg Kh-rf-graph-5.jpg




Bearbeite folgende Übungen: 

Halte beim Anklicken die Shift-Taste gedrückt, dann öffnet sich der Link in einem neuen Fenster!
  30px   Aufgabe 1

Ordne den richtigen Term den gezeigten Graphen zu.

  30px   Aufgabe 2

Ordne den richtigen Graph und angegebenen Termen zu.

  30px   Aufgabe 3

Gib zu den Graphen bzw. Termen die richtige Definitionsmenge an.

  30px   Aufgabe 4

Gib zu den Graphen bzw. Termen die Asymptoten an.]

  30px   Aufgabe 5

Memory-Quiz

  30px   Aufgabe 6

Knobel-Aufgaben

Von „http://rsg.zum.de/index.php?title=M8_-_Tests_zu_gebrochen-rationalen_Funktionen&oldid=9077“