Abiturwissen Mathematik: Unterschied zwischen den Versionen
(→Analysis) |
(→Geometrie) |
||
| Zeile 46: | Zeile 46: | ||
=Geometrie= | =Geometrie= | ||
| + | |||
| + | [[Datei:neu.jpg]] Wie findet man die Ebenengleichung in Parameterform, wenn ein Punkt P der Ebene und der Normalenvektor <math>\vec{n}</math> der Ebene gegeben sind? | ||
| + | |||
| + | Als Stützvektor nimmt man den Ortsvektor des gegebenen Punktes P. Nun braucht man noch zwei Richtungsvektoren <math>\vec{u}</math> und <math>\vec{v}</math>. Das Vektorprodukt hilft uns hier nicht weiter. Man erhält die Richtungsvektoren mit folgendem Trick:<br> | ||
| + | 1. Eine Komponente des Normalenvektors 0 setzen. <br> | ||
| + | 2. Die anderen beiden Komponenten vertauschen.<br> | ||
| + | 3. Eine der beiden vertauschten Komponenten negieren. | ||
| + | |||
| + | '''Beispiel:''' P(5;1;2) und <math>\vec{n}=\left( \begin{array}{c} 1 \\\ 3 \\\ -2 \end{array}\right)</math> | ||
| + | |||
| + | 1. x<sub>1</sub>- und x<sub>2</sub>-Komponente werden 0 gesetzt.<br> | ||
| + | <math>\left( \begin{array}{c} 0 \\\ 3 \\\ -2 \end{array}\right)</math> und <math>\left( \begin{array}{c} 1 \\\ 0 \\\ -2 \end{array}\right)</math> | ||
| + | |||
| + | 2. Die anderen beiden Komponenten werden jeweils vertauscht.<br> | ||
| + | |||
| + | <math>\left( \begin{array}{c} 0 \\\ -2 \\\ 3 \end{array}\right)</math> und <math>\left( \begin{array}{c} -2 \\\ 0 \\\ 1 \end{array}\right)</math> | ||
| + | |||
| + | 3. Eine der beiden vertauschen Komponenten wird negiert. | ||
| + | |||
| + | <math>\left( \begin{array}{c} 0 \\\ 2 \\\ 3 \end{array}\right)</math> und <math>\left( \begin{array}{c} 2 \\\ 0 \\\ 1 \end{array}\right)</math><br> | ||
| + | Damit sind die Richtungsvektoren der Ebene <math>\vec{u}=\left( \begin{array}{c} 0 \\\ 2 \\\ 3 \end{array}\right)</math> und <math>\vec{v}=\left( \begin{array}{c} 2 \\\ 0 \\\ 1 \end{array}\right)</math> . | ||
| + | |||
| + | Dies liefert die Parametergleichung der Ebene E: <math> \vec{x}=\left( \begin{array}{c} 5 \\\ 1 \\\ 2 \end{array}\right) + m | ||
| + | \left( \begin{array}{c} 0 \\\ 2 \\\ 3 \end{array}\right) + n \left( \begin{array}{c} 2 \\\ 0 \\\ 1 \end{array}\right) </math> | ||
| + | |||
| + | Man sieht, dass die Skalarprodukte <math>\vec{n} \circ \vec{u}</math> und <math>\vec{n} \circ \vec{v}</math> jeweils 0 sind, also stehen die Richtungsvektoren <math>\vec{u}</math> und <math>\vec{v}</math> senkrecht zum Normalenvektor <math>\vec{n}</math>. | ||
Version vom 16. April 2020, 10:01 Uhr
Inhaltsverzeichnis |
Was man im Abitur wissen sollte
Es kommen im Abitur viele Sachen aus den unteren Klassen vor. Mit den Links auf der Seite
kann man vorhandene Lücken aufarbeiten.
Bei Mathematik_Q11 und Mathematik_Q12 findet man viel zum aktuellen Stoff!
Im Weiteren findet ihr diverse Inhalte, die man für das Abitur auch noch wiederholen kann:
Abituraufgaben
- Abituraufgaben der letzten Jahre - Aufgaben, Lösungen, Videos in denen ein Lehrer die Aufgaben vorrechnet. Man muss sich aber vorher anmelden.
- Die Aufgaben beim ISB
Analysis
- Einfluss der Parameter
bei quadratischen Funktionen Scheitelform und allgemeine Form
bei trigonometrischen Funktionen
bei Wurzelfunktionen
- Das logarithmische Integrieren als Video oder hier (Seite 1) und Aufgaben 1- 12
Stochastik
- Pfadregeln:
Die Pfadregeln
Die Pfadregeln mit Beispielen
Aufgaben 1 und 2 mit Lösungen, 3
Geometrie
Wie findet man die Ebenengleichung in Parameterform, wenn ein Punkt P der Ebene und der Normalenvektor 
der Ebene gegeben sind?
Als Stützvektor nimmt man den Ortsvektor des gegebenen Punktes P. Nun braucht man noch zwei Richtungsvektoren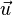 
und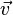 
. Das Vektorprodukt hilft uns hier nicht weiter. Man erhält die Richtungsvektoren mit folgendem Trick:
1. Eine Komponente des Normalenvektors 0 setzen.
2. Die anderen beiden Komponenten vertauschen.
3. Eine der beiden vertauschten Komponenten negieren.
Beispiel: P(5;1;2) und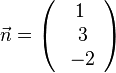 
1. x1- und x2-Komponente werden 0 gesetzt.
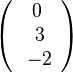und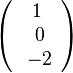 
2. Die anderen beiden Komponenten werden jeweils vertauscht.
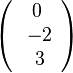und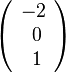 
3. Eine der beiden vertauschen Komponenten wird negiert.
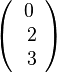und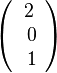 
Damit sind die Richtungsvektoren der Ebene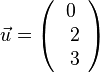 
und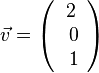 
.
Dies liefert die Parametergleichung der Ebene E: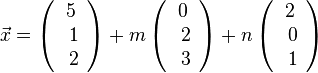 
Man sieht, dass die Skalarprodukte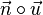 
und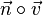 
jeweils 0 sind, also stehen die Richtungsvektoren 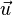und 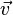senkrecht zum Normalenvektor .
