M11 Betrag eines Vektors: Unterschied zwischen den Versionen
| Zeile 102: | Zeile 102: | ||
Die Umfangslänge ist <math>U=3\sqrt 2 + 6 + 3\sqrt {6}=6+3(\sqrt 2 + \sqrt 6)</math> }} | Die Umfangslänge ist <math>U=3\sqrt 2 + 6 + 3\sqrt {6}=6+3(\sqrt 2 + \sqrt 6)</math> }} | ||
| − | + | '''Aufgaben zur Kugel''' | |
| − | + | ||
| − | {{ | + | {{Aufgaben-blau|6|2=HA Buch S. 106 / 10 }} |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Version vom 19. Januar 2021, 12:29 Uhr
|
Merke:
Der Betrag Die Entfernung zweier Punkte P und Q ist der Betrag des Vektors 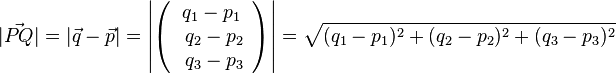 |
a) 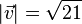
b) 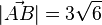
c) 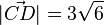
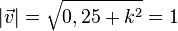 , also 0,25 + k² =1 liefert
, also 0,25 + k² =1 liefert 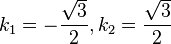
|
Merke:
Ein Vektor mit dem Betrag 1 heißt Einheitsvektor. |
1. Der Betrag des Vektors 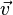 ist
ist 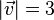 .
.
a) 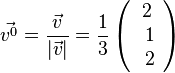
b) 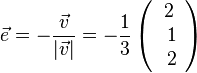
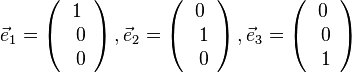
|
Merke:
Alle Punkte X(x1,x2,x3) im Raum, die von einem Punkt M(m1,m2,m3) die gleiche Entfernung r haben bilden die Oberfläche einer Kugel K. Für die Punkte X gilt: Die Gleichung |
a) 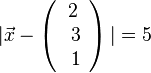 und
und 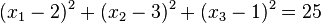
b) 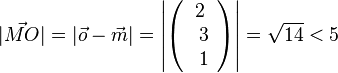 , also liegt O innerhalb der Kugel.
, also liegt O innerhalb der Kugel.
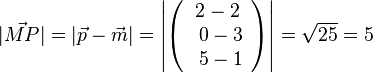 , also liegt P auf der Kugel.
, also liegt P auf der Kugel.
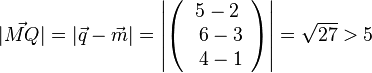 , also liegt Q außerhalb der Kugel.
, also liegt Q außerhalb der Kugel.
105/1a 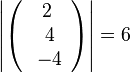
g) 1
105/2a) 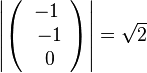
b) 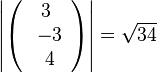
c) 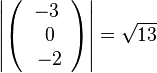
d) 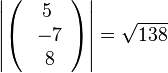
e) 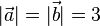 , also
, also 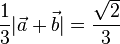
f) 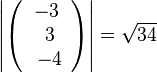
105/4 a) 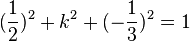 liefert
liefert 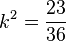 , also
, also 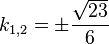
b) k = -1
c) es gibt kein k
d) 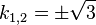
e) 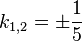
f) 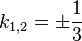
105/5a 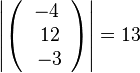 , also
, also 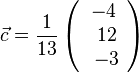
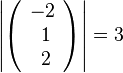 , also
, also 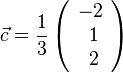
105/3 a) den Betrag 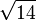 haben die Vektoren
haben die Vektoren 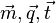 , den Betrag 2 haben die Vektoren
, den Betrag 2 haben die Vektoren 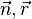 , den Betrag
, den Betrag 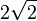 haben die Vektoren
haben die Vektoren 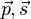
b) zueinander parallel sind 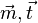 und
und 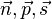
c) Gegenvektoren sind 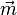 und
und 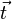 , sowie
, sowie 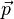 und
und 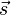 .
.
d) gleich sind keine der Vektoren
106/7a) 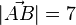
b) 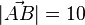
c) 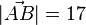
106/8 a) 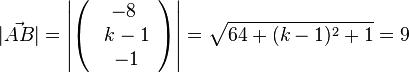 , also
, also 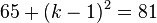 -->
--> 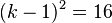 dies liefert zwei Lösungen
dies liefert zwei Lösungen
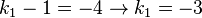 und
und 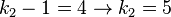
b) k1=3 und k2=7
106/9 Die Dreiecksseiten sind 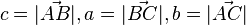
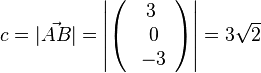
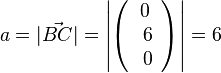
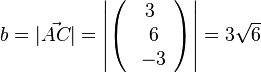
Ein Dreieck ist rechtwinklig, wenn der Satz des Pythagoras gilt: 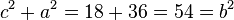 , also ist das Dreieck ABC bei B rechtwinklig.
, also ist das Dreieck ABC bei B rechtwinklig.
Der Flächeninhalt ergibt sich zu 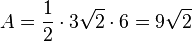
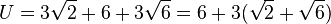
Aufgaben zur Kugel

 des Vektors
des Vektors 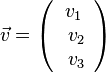 ist
ist 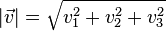 .
.
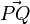 .
.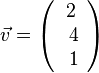 ?
?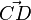 für C(-5;3,-1) und D(2;4;1).
für C(-5;3,-1) und D(2;4;1).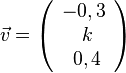 den Betrag 1?
den Betrag 1?
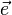 bezeichnet.
bezeichnet. 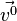 bezeichnet. Es ist
bezeichnet. Es ist 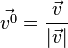
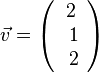 .
.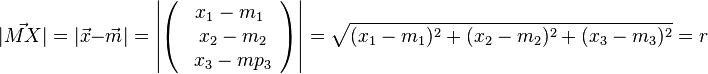
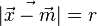 ist die Vektorgleichung,
ist die Vektorgleichung, 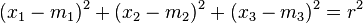 die Koordinatengleichung einer Kugel.
die Koordinatengleichung einer Kugel.

