M11 Betrag eines Vektors: Unterschied zwischen den Versionen
| Zeile 135: | Zeile 135: | ||
<math>(x_1+1)^2+(x_2-3)^2 +x_3^2 -1 = 0</math> oder <math>(x_1+1)^2+(x_2-3)^2 +x_3^2 = 1 </math><br> | <math>(x_1+1)^2+(x_2-3)^2 +x_3^2 -1 = 0</math> oder <math>(x_1+1)^2+(x_2-3)^2 +x_3^2 = 1 </math><br> | ||
Das ist die Gleichung einer Kugel mit M(-1;3;0) und r = 1.<br> | Das ist die Gleichung einer Kugel mit M(-1;3;0) und r = 1.<br> | ||
| − | g) Man kann die Gleichung umformen in <math>(x_1-8)^2+(x_2+4)^2-(x_3-3)^2=289</math>. Das ist die Gleichung einer Kugel mit M( | + | g) Man kann die Gleichung umformen in <math>(x_1-8)^2+(x_2+4)^2-(x_3-3)^2=289</math>. Das ist die Gleichung einer Kugel mit M(8;-4;3) und r = 17. <br> |
h) Man kann die Gleichung umformen in <math>(x_1+4)^2+x_2^2+x_3^2=25</math>. Das ist die Gleichung einer Kugel mit M(-4,0,0) und r=5.<br> | h) Man kann die Gleichung umformen in <math>(x_1+4)^2+x_2^2+x_3^2=25</math>. Das ist die Gleichung einer Kugel mit M(-4,0,0) und r=5.<br> | ||
| − | i) Man kann die Gleichung umformen in <math> | + | i) Man kann die Gleichung umformen in <math>(x_1-1)^2+(x_2-5)^2+(x_3+1)^2=81</math>. Das ist die Gleichung einer Kugel mit M(1;5;-1) und r=2. }} |
Version vom 20. Januar 2021, 08:25 Uhr
|
Merke:
Der Betrag Die Entfernung zweier Punkte P und Q ist der Betrag des Vektors 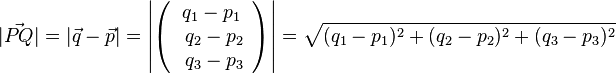 |
a) 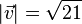
b) 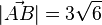
c) 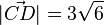
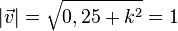 , also 0,25 + k² =1 liefert
, also 0,25 + k² =1 liefert 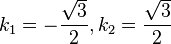
|
Merke:
Ein Vektor mit dem Betrag 1 heißt Einheitsvektor. |
1. Der Betrag des Vektors 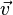 ist
ist 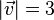 .
.
a) 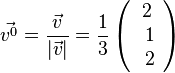
b) 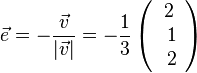
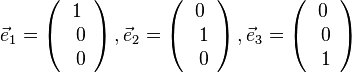
|
Merke:
Alle Punkte X(x1,x2,x3) im Raum, die von einem Punkt M(m1,m2,m3) die gleiche Entfernung r haben bilden die Oberfläche einer Kugel K. Für die Punkte X gilt: Die Gleichung |
a) 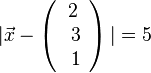 und
und 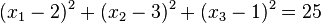
b) 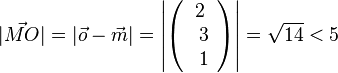 , also liegt O innerhalb der Kugel.
, also liegt O innerhalb der Kugel.
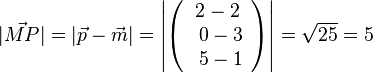 , also liegt P auf der Kugel.
, also liegt P auf der Kugel.
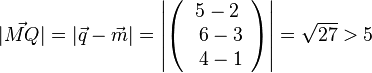 , also liegt Q außerhalb der Kugel.
, also liegt Q außerhalb der Kugel.
105/1a 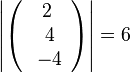
g) 1
105/2a) 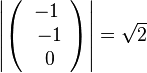
b) 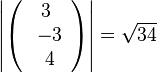
c) 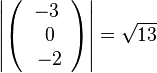
d) 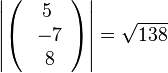
e) 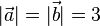 , also
, also 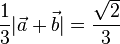
f) 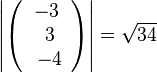
105/4 a) 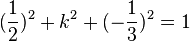 liefert
liefert 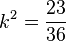 , also
, also 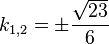
b) k = -1
c) es gibt kein k
d) 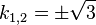
e) 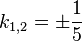
f) 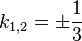
105/5a 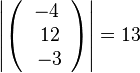 , also
, also 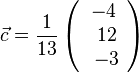
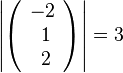 , also
, also 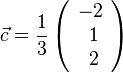
105/3 a) den Betrag 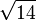 haben die Vektoren
haben die Vektoren 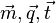 , den Betrag 2 haben die Vektoren
, den Betrag 2 haben die Vektoren 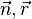 , den Betrag
, den Betrag 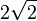 haben die Vektoren
haben die Vektoren 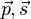
b) zueinander parallel sind 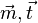 und
und 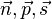
c) Gegenvektoren sind 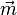 und
und 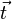 , sowie
, sowie 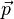 und
und 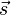 .
.
d) gleich sind keine der Vektoren
106/7a) 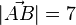
b) 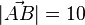
c) 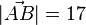
106/8 a) 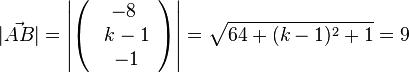 , also
, also 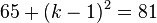 -->
--> 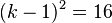 dies liefert zwei Lösungen
dies liefert zwei Lösungen
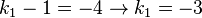 und
und 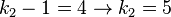
b) k1=3 und k2=7
106/9 Die Dreiecksseiten sind 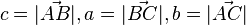
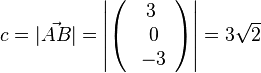
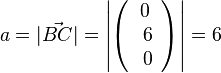
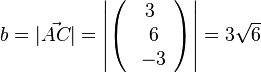
Ein Dreieck ist rechtwinklig, wenn der Satz des Pythagoras gilt: 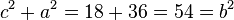 , also ist das Dreieck ABC bei B rechtwinklig.
, also ist das Dreieck ABC bei B rechtwinklig.
Der Flächeninhalt ergibt sich zu 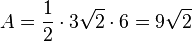
Aufgaben zur Kugel
106/11 a) Es ist 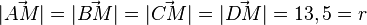
Koordinatengleichung: 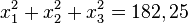 ; Vektorgleichung:
; Vektorgleichung: 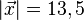
b) Es ist 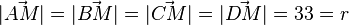
Koordinatengleichung: 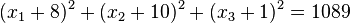 ; Vektorgleichung:
; Vektorgleichung: 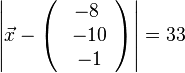 oder
oder 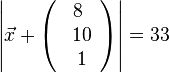
106/12a) 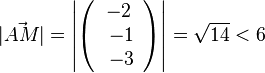 , A liegt innerhalb der Kugel.
, A liegt innerhalb der Kugel.
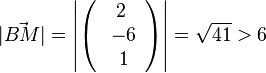 , B liegt außerhalb der Kugel.
, B liegt außerhalb der Kugel.
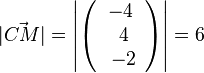 , C liegt auf der Kugel.
, C liegt auf der Kugel.
106/13a) ist eine Kugelgleichung mit M(3;0;-2) und r = 2
b) ist eine Kugelgleichung mit M(-3;4;2) und r O 13
c) ist keine Kugelgleichung (wenn man -1 auf die rechte Seite bringt ist auf der linken Seite die Summe von Quadraten, die nie -1 werden kann)
d) ist eine Kugelgleichung mit M(4;0;-2) und r = 8
f) ist eine Kugelgleichung mit M(0;0;0) und r = 2
Nun muss man wirklich rechnen :-(
e) Die Gleichung 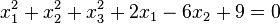 muss man jetzt in Koordinatenform bringen. Das erfolgt mit quadratischer Ergänzung.
muss man jetzt in Koordinatenform bringen. Das erfolgt mit quadratischer Ergänzung.
Dazu schreibt man zuerst die Gleichung in dieser Form: 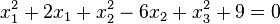 und ergänzt "mit 0"
und ergänzt "mit 0"
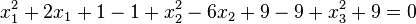
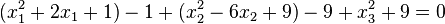 Die Klammern sind mit den binomischen Formeln Quadrate.
Die Klammern sind mit den binomischen Formeln Quadrate.
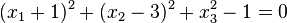 oder
oder 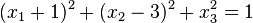
Das ist die Gleichung einer Kugel mit M(-1;3;0) und r = 1.
g) Man kann die Gleichung umformen in 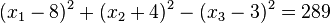 . Das ist die Gleichung einer Kugel mit M(8;-4;3) und r = 17.
. Das ist die Gleichung einer Kugel mit M(8;-4;3) und r = 17.
h) Man kann die Gleichung umformen in 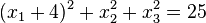 . Das ist die Gleichung einer Kugel mit M(-4,0,0) und r=5.
. Das ist die Gleichung einer Kugel mit M(-4,0,0) und r=5.
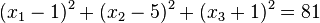 . Das ist die Gleichung einer Kugel mit M(1;5;-1) und r=2.
. Das ist die Gleichung einer Kugel mit M(1;5;-1) und r=2.
 des Vektors
des Vektors 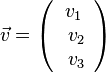 ist
ist 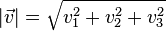 .
.
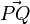 .
.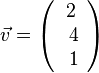 ?
?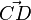 für C(-5;3,-1) und D(2;4;1).
für C(-5;3,-1) und D(2;4;1).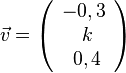 den Betrag 1?
den Betrag 1?
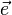 bezeichnet.
bezeichnet. 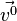 bezeichnet. Es ist
bezeichnet. Es ist 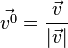
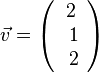 .
.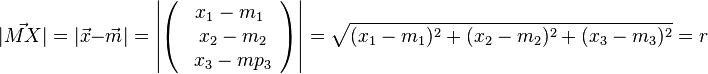
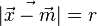 ist die Vektorgleichung,
ist die Vektorgleichung, 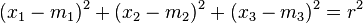 die Koordinatengleichung einer Kugel.
die Koordinatengleichung einer Kugel.

