M11 Betrag eines Vektors: Unterschied zwischen den Versionen
| Zeile 12: | Zeile 12: | ||
b) <math>|\vec {AB}|=3\sqrt 6</math> <br> | b) <math>|\vec {AB}|=3\sqrt 6</math> <br> | ||
c) <math>|\vec {CD}|=3\sqrt 6</math> <br> | c) <math>|\vec {CD}|=3\sqrt 6</math> <br> | ||
| − | d) <math>|\vec v |=\sqrt{0,25 +k^2}=1</math>, also 0,25 + k² =1 liefert<math>k_1=-\frac{\sqrt 3}{2}, k_2=\frac{\sqrt 3}{2}</math> | + | d) <math>|\vec v |=\sqrt{0,25 +k^2}=1</math>, also 0,25 + k² =1 liefert <math>k_1=-\frac{\sqrt 3}{2}, k_2=\frac{\sqrt 3}{2}</math> }} |
| Zeile 47: | Zeile 47: | ||
<math>| \vec {MP} |=|\vec p - \vec m|= \left | \left ( \begin{array}{c} 2-2 \\\ 0-3 \\\ 5-1 \end{array}\right) \right| = \sqrt{25} = 5</math>, also liegt P auf der Kugel.<br> | <math>| \vec {MP} |=|\vec p - \vec m|= \left | \left ( \begin{array}{c} 2-2 \\\ 0-3 \\\ 5-1 \end{array}\right) \right| = \sqrt{25} = 5</math>, also liegt P auf der Kugel.<br> | ||
<math>| \vec {MQ} |=|\vec q - \vec m|= \left | \left ( \begin{array}{c} 5-2 \\\ 6-3 \\\ 4-1 \end{array}\right) \right| = \sqrt{27} >5</math>, also liegt Q außerhalb der Kugel. }} | <math>| \vec {MQ} |=|\vec q - \vec m|= \left | \left ( \begin{array}{c} 5-2 \\\ 6-3 \\\ 4-1 \end{array}\right) \right| = \sqrt{27} >5</math>, also liegt Q außerhalb der Kugel. }} | ||
| + | |||
| + | |||
| + | {{Aufgaben-blau|4|2=Buch S. 105 / 1a,g<br> | ||
| + | Buch S. 105 / 2<br> | ||
| + | Buch S. 105 / 4 }} | ||
| + | |||
| + | {{Lösung versteckt|1=105/1a <math>\left | \left ( \begin{array}{c} 2 \\\ 4 \\\ -4 \end{array}\right) \right| = 6</math><br> | ||
| + | g) 1 | ||
| + | |||
| + | 105/2a) <math>\left | \left ( \begin{array}{c} -1 \\\ -1 \\\ 0 \end{array}\right) \right|=\sqrt 2</math><br> | ||
| + | b) <math>\left | \left ( \begin{array}{c} 3 \\\ -3 \\\ 4 \end{array}\right) \right| =\sqrt {34}</math><br> | ||
| + | c) <math>\left | \left ( \begin{array}{c} -3 \\\ 0 \\\ -2 \end{array}\right) \right| = \sqrt {13}</math><br> | ||
| + | d) <math>\left | \left ( \begin{array}{c} 5 \\\ -7 \\\ 8 \end{array}\right) \right| =\sqrt {138}</math><br> | ||
| + | e) <math>| \vec a |=| \vec b| = 3</math>, also <math>\frac{1}{3}|\vec a + \vec b|=\frac{\sqrt 2}{3}</math><br> | ||
| + | f) <math>\left | \left ( \begin{array}{c} -3 \\\ 3 \\\ -4 \end{array}\right) \right| =\sqrt {34}</math> | ||
| + | |||
| + | 105/4 a) <math>(\frac{1}{2})^2 + k^2 + (-\frac{1}{3})^2=1</math> liefert <math>k^2 = \frac{23}{36}</math>, also <math>k_{1,2}=\pm \frac{\sqrt{23}}{6}</math><br> | ||
| + | b) k = -1<br> | ||
| + | c) es gibt kein k<br> | ||
| + | d) <math>k_{1,2}=\pm \sqrt 3</math><br> | ||
| + | e) <math>k_{1,2}=\pm \frac{1}{5}</math><br> | ||
| + | f) <math>k_{1,2}=\pm \frac{1}{3}</math> | ||
| + | }} | ||
Version vom 19. Januar 2021, 09:11 Uhr
|
Merke:
Der Betrag Die Entfernung zweier Punkte P und Q ist der Betrag des Vektors 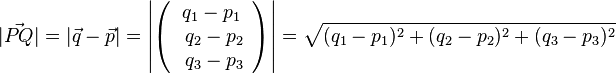 |
a) 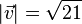
b) 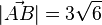
c) 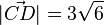
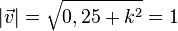 , also 0,25 + k² =1 liefert
, also 0,25 + k² =1 liefert 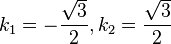
|
Merke:
Ein Vektor mit dem Betrag 1 heißt Einheitsvektor. |
1. Der Betrag des Vektors 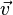 ist
ist 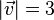 .
.
a) 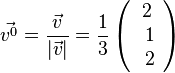
b) 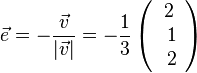
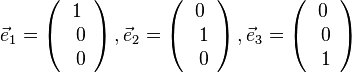
|
Merke:
Alle Punkte X(x1,x2,x3) im Raum, die von einem Punkt M(m1,m2,m3) die gleiche Entfernung r haben bilden die Oberfläche einer Kugel K. Für die Punkte X gilt: Die Gleichung |
a) 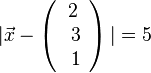 und
und 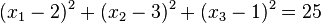
b) 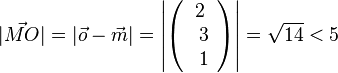 , also liegt O innerhalb der Kugel.
, also liegt O innerhalb der Kugel.
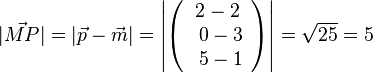 , also liegt P auf der Kugel.
, also liegt P auf der Kugel.
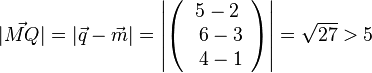 , also liegt Q außerhalb der Kugel.
, also liegt Q außerhalb der Kugel.
105/1a 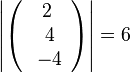
g) 1
105/2a) 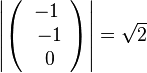
b) 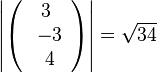
c) 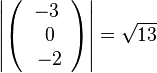
d) 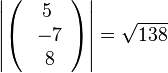
e) 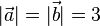 , also
, also 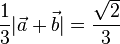
f) 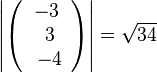
105/4 a) 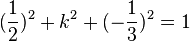 liefert
liefert 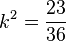 , also
, also 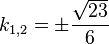
b) k = -1
c) es gibt kein k
d) 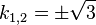
e) 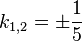
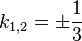

 des Vektors
des Vektors 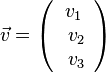 ist
ist 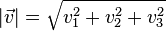 .
.
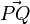 .
.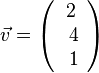 ?
?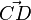 für C(-5;3,-1) und D(2;4;1).
für C(-5;3,-1) und D(2;4;1).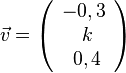 den Betrag 1?
den Betrag 1?
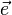 bezeichnet.
bezeichnet. 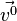 bezeichnet. Es ist
bezeichnet. Es ist 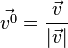
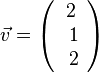 .
.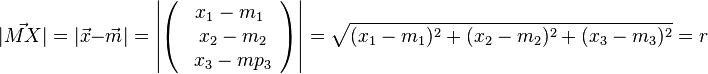
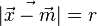 ist die Vektorgleichung,
ist die Vektorgleichung, 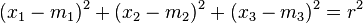 die Koordinatengleichung einer Kugel.
die Koordinatengleichung einer Kugel.

