2018-19-M-Hab
Inhaltsverzeichnis |
Wiederholung
Grundlegende Fertigkeiten, die man zu Beginn der Oberstufe haben sollte
Aufgaben: Binomische Formeln, Binomische Formeln 2
Übungsblatt zum Wiederholen
Geradengleichungen, Gerdengleichung erstellen,
Mitternachtsformel, Quadratische Gleichungen, Quadratische Gleichungen 2
Gebrochen-rationale Funktionen
Gebrochen-rationale_Funktionen
Die Ableitungsfunktion
Von der Sekantensteigung zur Tangentensteigung:
Mit dem Schieberegler für h kann man den x-Abstand h des Punktes B vom Punkt A ändern. Geht h gegen 0 so wird aus der Sekante [AB] die Tangente in A an den Graphen der Funktion f.
Lernpfad: Einführung in die Differentialrechnung
Wissen:Ableitung, Differentialquotient
Die Ableitungsfunktion f'
Gegeben ist die Polynomfunktion 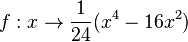 .
.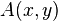 ist ein Punkt auf dem Graphen von
ist ein Punkt auf dem Graphen von  . In
. In 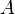 ist die Tangente an den Graphen von
ist die Tangente an den Graphen von  , diese hat die Steigung
, diese hat die Steigung 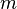 . Trägt man über jeden x-Wert von
. Trägt man über jeden x-Wert von 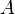 den Steigungswert
den Steigungswert 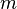 an, so erhält man den Punkt
an, so erhält man den Punkt 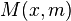 . Bewegt man nun den Punkt
. Bewegt man nun den Punkt 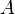 auf dem Graphen von
auf dem Graphen von  so variiert auch der Punkt
so variiert auch der Punkt 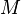 und die Spur des Punktes
und die Spur des Punktes 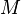 gibt den Graphen der Ableitungsfunktion
gibt den Graphen der Ableitungsfunktion 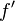 wieder.
wieder.
Zusammenhang zwischen Funktion und 1. Ableitung
Überblick über die Ableitungsregeln mit Beispielen
multiple-choice
Ableitungspuzzle
Produkt- und Quotientenregel
Aufgaben zur Quotientenregel
Musteraufgabe zur Kurvendiskussion
Wiederholungsaufgaben: Aufgaben zum Differentialquotienten,
Aufgaben zu Produkt- und Quotientenregel
Polynomfunktionen - Ableitung, Monotonie, Extremwerte,
Das Newton-Verfahren
So geht es, Applet zur Veranschaulichung
Zusatzaufgaben
Differenzen-und Differentialquotient
Ableitungsfunktion
Ableitungsregeln I
Tangenten und Normalen
Extremwerte
Das Newton-Verfahren
So geht es, Applet zur Veranschaulichung
Verkettung von Funktionen
Die Ableitung der trigonometrischen Funktionen
Wiederholung aus der 10. Klasse
Ableitung der Winkelfunktionen mit Beweis! und Beispielen
Die Umkehrfunktion
* Die Umkehrfunktion
Ableitung der Exponential- und Logarithmusfunktionen
Ableitung der e-Funktion
Beispiele
Zusammenfassung der Ableitungsregeln und Ableitungen verschiedener Funktionen
Stochastik
Bedingte Wahrscheinlichkeiten
Stochastische Unabhängigkeit
Zusammenfassung und Aufgaben zur Unabhängigkeit von Ereignissen

