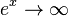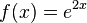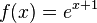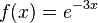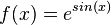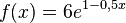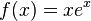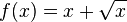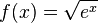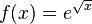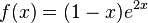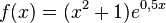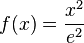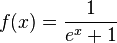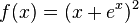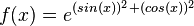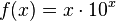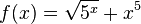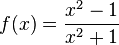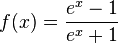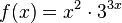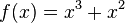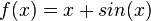M11 Ableitung der Exponentialfunktionen: Unterschied zwischen den Versionen
| (2 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 30: | Zeile 30: | ||
<center><math> (a^x)' = ln(a) \cdot a^x</math>.</center> }} | <center><math> (a^x)' = ln(a) \cdot a^x</math>.</center> }} | ||
| − | {{Merke|1=Eigenschaften der e-Funktion | + | {{Merke|1=Eigenschaften der e-Funktion (natürliche Exponentialfunktion) <math>f:x \rightarrow e^x</math> [[Datei:e-funktion.jpg|thumb|350px]] |
* D = R, W = R<sup>+</sup><br> | * D = R, W = R<sup>+</sup><br> | ||
| − | < | + | * e<sup>x</sup> > 0 |
| − | + | ||
| − | + | ||
* Der Graph geht durch den Punkt (0;1)<br> | * Der Graph geht durch den Punkt (0;1)<br> | ||
| + | |||
| + | * f(1) = e | ||
* Der Graph der e-Funktion ist streng montoton steigend. | * Der Graph der e-Funktion ist streng montoton steigend. | ||
| − | * Die negative x-Achse ist | + | * Die negative x-Achse ist Asymptote. |
| + | |||
| + | * Für <math>x \to \infty</math> ist <math>e^x \to \infty</math>}} | ||
Aktuelle Version vom 19. März 2021, 14:59 Uhr
|
Merke:
Die Funktion 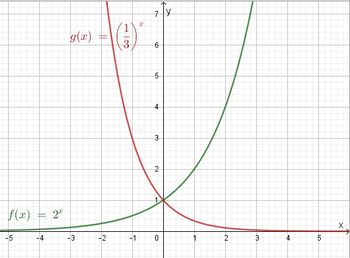 Der Graph ist eine Exponentialkurve. |
Für die Ableitung der Exponentialfunktion zur Basis a geht man auf die Definition zurück:
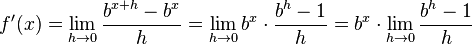 .
.
Löst man die Gleichung 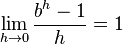 nach b auf, so erhält man
nach b auf, so erhält man 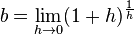 . Wenn
. Wenn  ist, dann ist
ist, dann ist 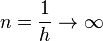 und man kann mittels einer Tabellenkalkulation den Grenzwert
und man kann mittels einer Tabellenkalkulation den Grenzwert 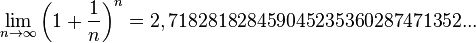 berechnen.
berechnen.
Dieser Grenzwert wird als Eulersche Zahl e bezeichnet. Es ist e = 2, 718 281 828 459 045 235 360 287 471 352 ... .
|
Merke:
Die Eulersche Zahl e ist definiert durch den Grenzwert Dies hat zur Folge, dass die Exponentialfunktion zur Basis e 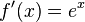 oder oder 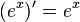 hat. Jede Funktion Die Gleichung
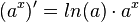 . . |
30px Merke
Eigenschaften der e-Funktion (natürliche Exponentialfunktion) 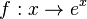
|
Beachten Sie die Ableitungsregeln, insbesondere die Kettenregel.
a) 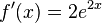
b) 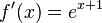
c) 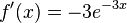
d) 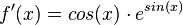
e) 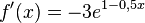
f) 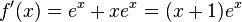
g) 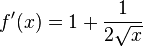
h) 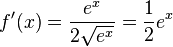
Dies hätte man auch erhalten, wenn man 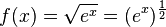 ableitet.
ableitet.
i) 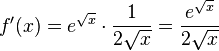
j) 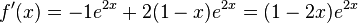
k) 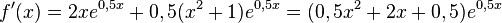
l) 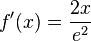 - Beachte e2 ist eine Zahl und hier steht keine Exponentialfunktion!
- Beachte e2 ist eine Zahl und hier steht keine Exponentialfunktion!
m) 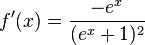
n) 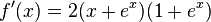
o) 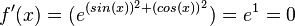
p) 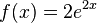
q) 
r) 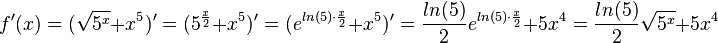
s) 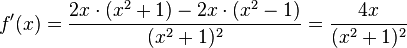
t) 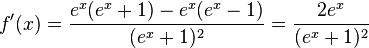
u) 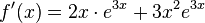
v) 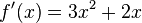
w) 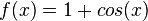
x) 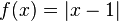
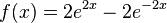 |
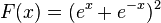
|
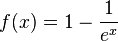 |
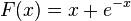
|
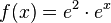 |
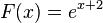
|
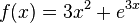 |
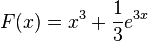
|
a) F(x) = ex + x + C
b) F(x) = -e-x + C
c) F(x) = 0,5(ex - e-x) + C
d) F(x) = 0,5x2 + 2x + ex+2 + C
e) F(x) = e1+x + C

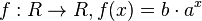 (b ∈ R+\{0}, a ∈ R+) heißt Exponentialfunktion zur Basis a.
(b ∈ R+\{0}, a ∈ R+) heißt Exponentialfunktion zur Basis a.
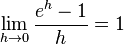 .
.
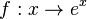 mit D = R und W = R+ die Ableitung
mit D = R und W = R+ die Ableitung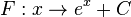 ist Stammfunktion von
ist Stammfunktion von  .
.
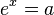 hat die Lösung
hat die Lösung 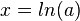 . Dabei ist
. Dabei ist 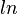 der Logarithmus zur Basis e und heißt natürlicher Logarithmus.
der Logarithmus zur Basis e und heißt natürlicher Logarithmus.
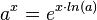 und der Kettenregel erhält man
und der Kettenregel erhält man 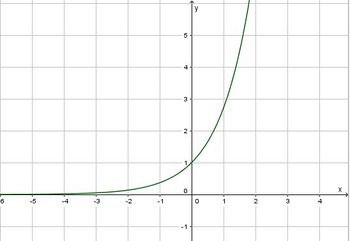
 ist
ist