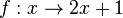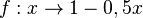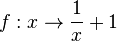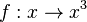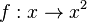Umkehrfunktion Beispiele: Unterschied zwischen den Versionen
| Zeile 1: | Zeile 1: | ||
| + | [[Die_Umkehrfunktion|Startseite]] - [[Umkehrfunktion_Wertetabelle|Wertetabelle]] - [[Umkehrfunktion_Graph|Graph]] - | ||
| + | [[Umkehrfunktion_Term|Term]] - [[Umkehrfunktion_Beispiele|Beispiele]] - [[Umkehrfunktion_Definitions-_und_Wertemenge|Definitions- und Wertemenge]] - [[Umkehrfunktion_Monotinie|Monotoniekriterium]] | ||
| + | ---- | ||
| + | |||
| + | |||
Um das bisher behandelte zu üben beginnen wir mit ähnlichen Beispielen, also linearen Funktionen | Um das bisher behandelte zu üben beginnen wir mit ähnlichen Beispielen, also linearen Funktionen | ||
| − | {{Aufgabe|Bestimme die Umkehrfunktion graphisch und rechnerisch der Funktion | + | {{Aufgabe| |
| + | Bestimme die Umkehrfunktion graphisch und rechnerisch der Funktion | ||
| − | + | a) <math>f: x \rightarrow 2x + 1</math> | |
| − | + | b) <math>f: x \rightarrow 1 -0,5x</math> | |
}} | }} | ||
{{Lösung versteckt| | {{Lösung versteckt| | ||
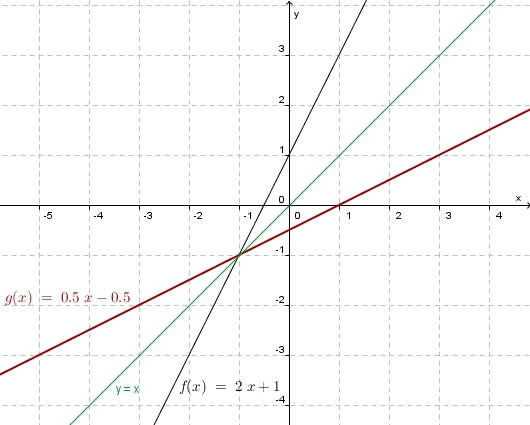
| − | + | a) '''Graphisch:<br>''' [[Bild:Funktion_umkf_bspl_1.jpg|400]] | |
'''Rechnerisch: ''' <math> y = 2 x + 1</math><br> | '''Rechnerisch: ''' <math> y = 2 x + 1</math><br> | ||
| Zeile 15: | Zeile 21: | ||
nach y auflösen: <math>y = \frac{1}{2}x-\frac{1}{2}</math> | nach y auflösen: <math>y = \frac{1}{2}x-\frac{1}{2}</math> | ||
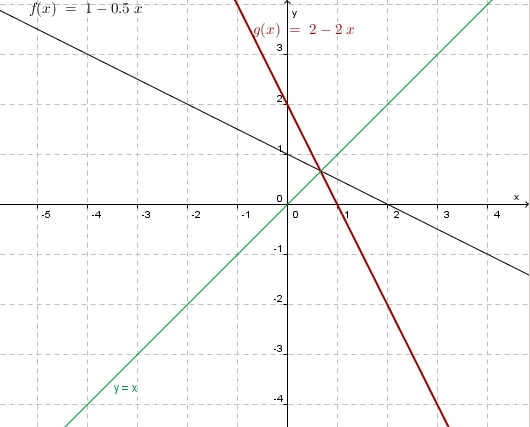
| − | + | b) '''Graphisch:<br>''' [[Bild:Funktion_umkf_bspl_2.jpg|400]] | |
'''Rechnerisch: ''' <math> y = 1 - 0,5 x</math><br> | '''Rechnerisch: ''' <math> y = 1 - 0,5 x</math><br> | ||
| Zeile 25: | Zeile 31: | ||
{{Aufgabe|Bestimme die Umkehrfunktion graphisch und algebraisch der Funktion | {{Aufgabe|Bestimme die Umkehrfunktion graphisch und algebraisch der Funktion | ||
| − | <math>f: x \rightarrow \frac{1}{x}+1</math> | + | |
| + | a) <math>f: x \rightarrow \frac{1}{x}+1</math> | ||
| + | |||
| + | b) <math>f: x \rightarrow x^3</math> | ||
| + | |||
| + | c) <math>f: x \rightarrow x^2</math> | ||
}} | }} | ||
{{Lösung versteckt| | {{Lösung versteckt| | ||
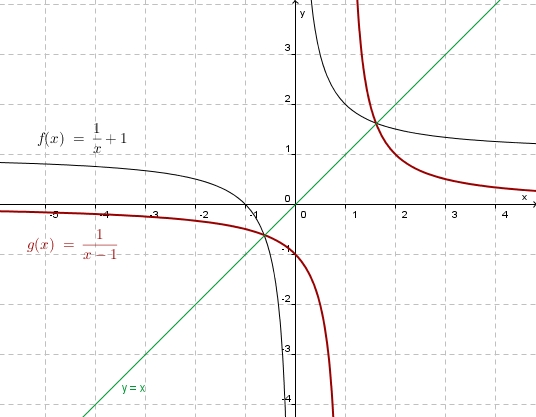
| − | '''Graphisch:<br>''' [[Bild:Funktion_umkf_bspl_3.jpg|400]] | + | a) '''Graphisch:<br>''' [[Bild:Funktion_umkf_bspl_3.jpg|400]] |
'''Rechnerisch: ''' <math> y =\frac{1}{x}+1</math><br> | '''Rechnerisch: ''' <math> y =\frac{1}{x}+1</math><br> | ||
x und y vertauschen: <math>x = \frac{1}{y}+1 </math><br> | x und y vertauschen: <math>x = \frac{1}{y}+1 </math><br> | ||
nach y auflösen: <math>y = \frac{1}{x-1}</math> | nach y auflösen: <math>y = \frac{1}{x-1}</math> | ||
| − | |||
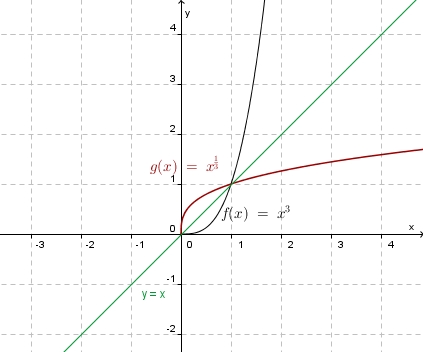
| − | + | b) '''Graphisch:<br>''' [[Bild:Funktion_umkf_bspl_4.jpg|400]] | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | '''Graphisch:<br>''' [[Bild:Funktion_umkf_bspl_4.jpg|400]] | + | |
'''Rechnerisch: ''' <math> y =x^3</math><br> | '''Rechnerisch: ''' <math> y =x^3</math><br> | ||
x und y vertauschen: <math>x = y^3 </math><br> | x und y vertauschen: <math>x = y^3 </math><br> | ||
nach y auflösen: <math>y = sqrt[3]{x}</math> | nach y auflösen: <math>y = sqrt[3]{x}</math> | ||
| − | |||
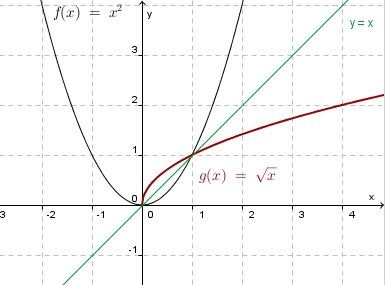
| − | + | c) '''Graphisch:<br>''' [[Bild:Funktion_umkf_bspl_5.jpg|400]] | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | '''Graphisch:<br>''' [[Bild:Funktion_umkf_bspl_5.jpg|400]] | + | |
'''Rechnerisch: ''' <math> y =x^2</math><br> | '''Rechnerisch: ''' <math> y =x^2</math><br> | ||
| Zeile 59: | Zeile 58: | ||
nach y auflösen: <math>y = sqrt{x}</math> | nach y auflösen: <math>y = sqrt{x}</math> | ||
}} | }} | ||
| + | |||
| + | |||
| + | Bei den letzten Aufgabe hat man ein Problem. Bei der graphischen Lösung geht man von einem Punkt der <math>y</math> waagrecht zum Funktionsgraph der Funktion <math>f</math> und von dort senkrecht zur <math>x</math>-Achse. Nur soll man von <math> y = 3</math> waagrecht losgehen? Nach links oder nach rechts? | ||
| + | |||
| + | <center>[[Bild:Funktion_umkf_bspl_5a.jpg]]</center> | ||
| + | |||
| + | Dies wollen wir bei [[Umkehrfunktion_Definitions-_und_Wertemenge|Definitions- und Wertemenge]] näher behandeln. | ||
Version vom 23. Mai 2012, 07:04 Uhr
Startseite - Wertetabelle - Graph - Term - Beispiele - Definitions- und Wertemenge - Monotoniekriterium
Um das bisher behandelte zu üben beginnen wir mit ähnlichen Beispielen, also linearen Funktionen
30px Aufgabe
Bestimme die Umkehrfunktion graphisch und rechnerisch der Funktion a) b) |
Rechnerisch: 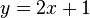
x und y vertauschen: 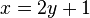
nach y auflösen: 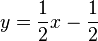
Rechnerisch: 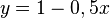
x und y vertauschen: 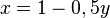
nach y auflösen: 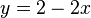
Nun wollen wir auch andere Funktionstypen untersuchen:
30px Aufgabe
Bestimme die Umkehrfunktion graphisch und algebraisch der Funktion a) b) c) |
Rechnerisch: 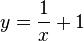
x und y vertauschen: 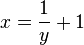
nach y auflösen: 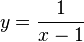
Rechnerisch: 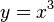
x und y vertauschen: 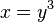
nach y auflösen: ![y = sqrt[3]{x}](/images/math/b/8/d/b8d31f8f5f7f9dca9e5988988e822131.png)
Rechnerisch: 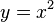
x und y vertauschen: 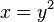
nach y auflösen: 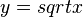
Bei den letzten Aufgabe hat man ein Problem. Bei der graphischen Lösung geht man von einem Punkt der 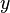 waagrecht zum Funktionsgraph der Funktion
waagrecht zum Funktionsgraph der Funktion  und von dort senkrecht zur
und von dort senkrecht zur 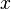 -Achse. Nur soll man von
-Achse. Nur soll man von 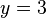 waagrecht losgehen? Nach links oder nach rechts?
waagrecht losgehen? Nach links oder nach rechts?
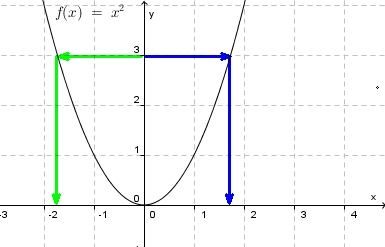
Dies wollen wir bei Definitions- und Wertemenge näher behandeln.