Umkehrfunktion Definitions- und Wertemenge: Unterschied zwischen den Versionen
| Zeile 19: | Zeile 19: | ||
Mit dieser Einschränkung der Definitionsmenge ist die umgekehrte Zuordnung wieder eindeutig und damit eine Funktion. | Mit dieser Einschränkung der Definitionsmenge ist die umgekehrte Zuordnung wieder eindeutig und damit eine Funktion. | ||
| − | Auf diesen Seiten wird dies nochmals erklärt:<br> | + | Auf diesen Seiten wird dies nochmals erklärt:<br> |
| − | [http://www.mathematik.net/Pot-fkt/Pw4s10.htm Potenzfunktionen mit geraden Exponenten haben eine Umkehrrelation]<br> | + | [http://www.mathematik.net/Pot-fkt/Pw4s10.htm Potenzfunktionen mit geraden Exponenten haben eine Umkehrrelation]<br> |
| − | [http://www.mathematik.net/Pot-fkt/Pw4s13.htm So findet man bei Potenzfunktionen mit geraden Exponenten die Umkehrfunktion] | + | [http://www.mathematik.net/Pot-fkt/Pw4s13.htm So findet man bei Potenzfunktionen mit geraden Exponenten die Umkehrfunktion] |
Alle Potenzfunktionen sind für <math>x \in R</math> definiert. Dies kann man bei der Bildung von Umkehrfunktionen nicht immer aufrecht erhalten. Potenzfunktionen mit ungeraden Exponenten kann man auch für <math>x \in R^-</math> umkehren, bei geraden Exponenten geht dies nicht. | Alle Potenzfunktionen sind für <math>x \in R</math> definiert. Dies kann man bei der Bildung von Umkehrfunktionen nicht immer aufrecht erhalten. Potenzfunktionen mit ungeraden Exponenten kann man auch für <math>x \in R^-</math> umkehren, bei geraden Exponenten geht dies nicht. | ||
Version vom 23. Mai 2012, 14:44 Uhr
Startseite - Wertetabelle - Graph - Term - Beispiele - Definitions- und Wertemenge - Monotoniekriterium
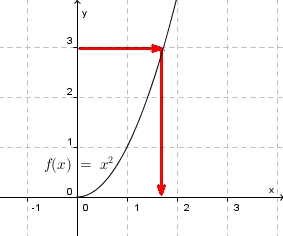
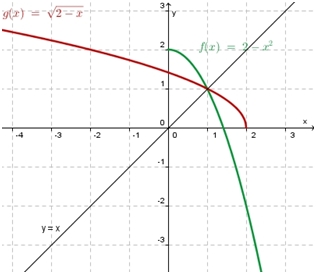
Im letzten Beispiel war nicht eindeutig, wie man die umgekehrte Zuordnung machen soll.
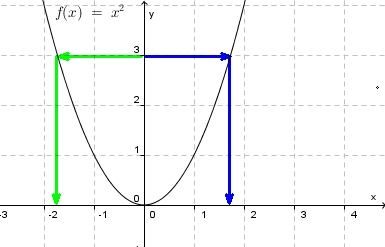
Man entscheidet sich für einen Weg, entweder nach links oder nach rechts. Wir gehen nach rechts und ignorieren den linken Teil der Parabel.
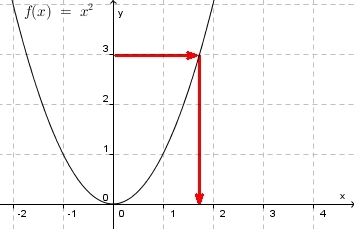
Man gehen davon aus, dass als Werte nur nicht negative Zahlen in Betracht kommen. Dies schränkt die Definitionsmenge der Funktions 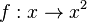 ein. Es ist dann
ein. Es ist dann 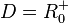 .
.
Mit dieser Einschränkung der Definitionsmenge ist die umgekehrte Zuordnung wieder eindeutig und damit eine Funktion.
Auf diesen Seiten wird dies nochmals erklärt:
Potenzfunktionen mit geraden Exponenten haben eine Umkehrrelation
So findet man bei Potenzfunktionen mit geraden Exponenten die Umkehrfunktion
Alle Potenzfunktionen sind für 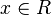 definiert. Dies kann man bei der Bildung von Umkehrfunktionen nicht immer aufrecht erhalten. Potenzfunktionen mit ungeraden Exponenten kann man auch für
definiert. Dies kann man bei der Bildung von Umkehrfunktionen nicht immer aufrecht erhalten. Potenzfunktionen mit ungeraden Exponenten kann man auch für 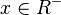 umkehren, bei geraden Exponenten geht dies nicht.
umkehren, bei geraden Exponenten geht dies nicht.
Hat man die Definitionsmenge 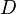 der Funktion
der Funktion  so eingeschränkt, dass die Umkehrung eine Funktion ist, dann gilt für die Definitionsmenge
so eingeschränkt, dass die Umkehrung eine Funktion ist, dann gilt für die Definitionsmenge 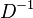 und Wertemenge
und Wertemenge 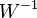 der Umkehrfunktion
der Umkehrfunktion 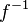 :
:
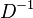 =
= 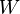 und
und 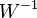 =
= 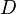 .
.
Funktion 
|
Funktion 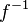
| |
| Definitionsmenge | 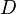
|
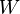
|
| Wertemenge | 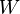
|
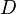
|
Dabei sind 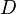 und
und 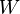 die Definitions- und Wertemenge der eingeschränkten Funktion
die Definitions- und Wertemenge der eingeschränkten Funktion  .
.
30px Aufgabe
Gib für die Funktion |
Ein einfaches Kriterium,wie man feststellt, dass eine Funktion  umkehrbar ist, ist das Monotoniekriterium .
umkehrbar ist, ist das Monotoniekriterium .
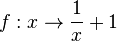
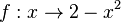
 bezeichnet.
bezeichnet.
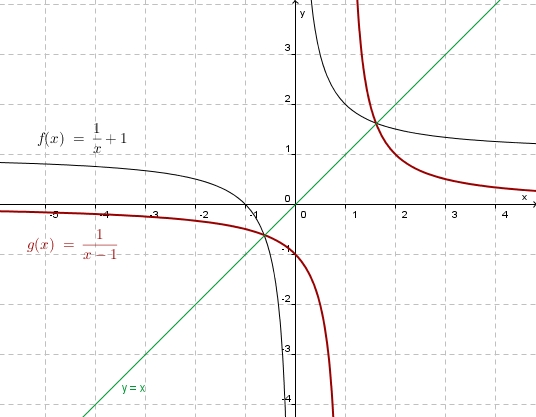
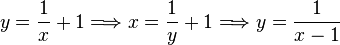 , also
, also 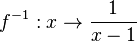 .
.
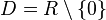 und
und 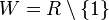 .
.
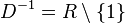 und
und 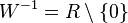 .
.
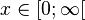 .
. 
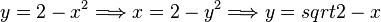 , also also
, also also 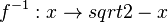 .
.
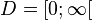 und
und ![W = ]-\infty;2]](/images/math/5/8/5/5851fda1d294c4d3288eb2a90b44b6b9.png) .
.
![D^{-1} = ]-\infty;2]](/images/math/c/1/f/c1f7344d24af0b1699f64b8d282fa700.png) und
und 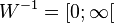 .
.

