Umkehrfunktion Monotonie: Unterschied zwischen den Versionen
| (5 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 17: | Zeile 17: | ||
| − | {{ | + | {{Aufgaben-blau|1|2=Teste dein Wissen über die Definition der Monotonie auf dieser [[Monotonie_Test|Seite]]. |
| + | }} | ||
| − | + | ||
| + | |||
| + | {{Merke| | ||
| + | Ist eine Funktion <math> f </math> im Intervall <math>[a;b]</math> streng monoton, dann ist sie in dem Intervall umkehrbar. | ||
}} | }} | ||
| − | |||
| − | |||
| − | |||
| − | + | {{Aufgaben-blau|2|2=Betrachte nun die Quadratfunktion <math> f: x\rightarrow x^2</math> mit <math>D = R</math>. | |
| − | + | ||
| − | + | 1. Wo ist die Quadratfunktion streng monoton abnehmend? Wo ist sie streng monoton zunehmend? | |
| − | + | ||
| − | + | 2. In welchen Intervallen ist die Quadratfunktion umkehrbar? | |
| − | + | ||
| − | + | 3. Gib für beide Intervalle die Umkehrfunktionen an. Zeichne jeweils die Graphen von eingeschränkter Funktion und Umkehrfunktion. | |
| − | + | ||
| − | + | }} | |
| − | + | ||
| − | + | {{Lösung versteckt| | |
| − | + | 1. Die Quadratfunktion ist im Intervall <math>]-\infty;0]</math> streng monoton abnehmend und im Intervall <math> [0;\infty[</math> streng monoton zunehmend. | |
| − | </ | + | 2. Der linke Ast ist für <math>x \in ]-\infty;0]</math> umkehrbar <br>. |
| + | Der rechte Ast ist für <math>x \in [0;\infty[</math> auch umkehrbar. | ||
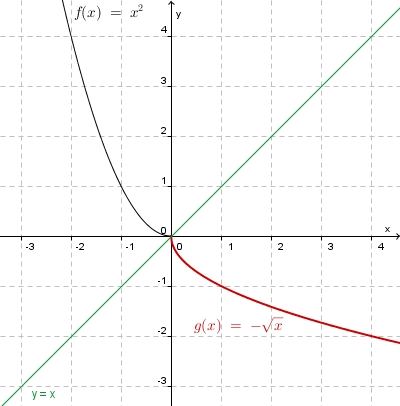
| + | 3. a) Für den linken Ast ist die Quadratfunktion <math>f</math> eingeschränkt mit <math>D = R^-_0 </math> und <math> W = R^+_0</math>. <br> | ||
| + | Die Umkehrfunktion ist <math>f^{-1}:x \rightarrow -\sqrt x </math> mit <math>D^{-1} = R^+_0 </math> und <math>W^{-1} = R^-_0</math>. | ||
| + | [[Bild:Umkfkt_quafkt_-.jpg]] | ||
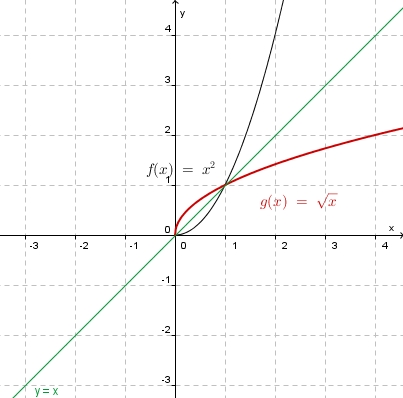
| − | + | 3. b) Für den rechten Ast ist die Quadratfunktion <math>f</math> eingeschränkt mit <math>D = R^+_0 </math> und <math> W = R^+_0</math><br> | |
| − | + | Die Umkehrfunktion <math>f^{-1}:x \rightarrow \sqrt x</math> mit <math>D^{-1} = R^+_0 </math> und <math>W^{-1} = R^+_0</math>. | |
| + | |||
| + | [[Bild:Umkfkt_quafkt_+.jpg]] | ||
}} | }} | ||
| + | {{Aufgaben-blau|3|2=Betrachte nun die Potenzfunktion <math> f: x \rightarrow x^3</math>. | ||
| + | 1. Gib Definitions- und Wertemenge an. | ||
| − | + | 2. Zeichne den Graphen der Funktion <math>f</math>. | |
| − | + | 3. Wo ist die Funktion streng monoton? | |
| − | + | 4. Bestimme die Umkehrfunktion zu f. Zeichne sie in das Diagramm von 2. | |
| + | }} | ||
| − | + | {{Lösung versteckt| | |
| − | + | 1. <math> D = R</math>, <math>W = R</math> | |
| − | + | 2. [[Bild:Umkfkt_kubikfkt.jpg]] | |
| − | + | ||
| − | + | 3. F ist streng monoton zunehmend in ganz <math>R</math>. | |
| − | + | 4. <math>f^{-1}: x \rightarrow \sqrt[3]x</math> mit <math> D^{-1} = R</math>, <math>W^{-1} = R</math> | |
| − | + | ||
| − | |||
}} | }} | ||
| + | |||
| + | {{Merke| | ||
| + | 1. Potenzfunktionen <math>f: x \rightarrow x^n</math> mit ungeraden Exponenten <math>n</math> sind in <math>R</math> umkehrbar. | ||
| + | |||
| + | Die Umkehrfunktion ist die n-Wurzelfunktion <math>f^{-1}: x \rightarrow \sqrt[n]x</math> mit <math> D^{-1} = R</math>, <math>W^{-1} = R</math>. | ||
| + | |||
| + | 2. Potenzfuntkionen <math>f: x \rightarrow x^n</math> mit geraden Exponenten <math>n</math> sind in <math>R</math> nicht umkehrbar. Sie müssen eingeschränkt werden, z.B. auf <math>R^+_0</math>. | ||
| + | |||
| + | Die Umkehrfunktion ist die n-Wurzelfunktion <math>f^{-1}: x \rightarrow \sqrt[n]x</math> mit <math> D^{-1} = R^+_0</math>, <math>W^{-1} = R^+_0</math>. | ||
| + | }} | ||
| + | |||
| + | |||
| + | |||
| + | ---- | ||
| + | Zurück zur [[Die_Umkehrfunktion|Startseite]] - [[Umkehrfunktion_Wertetabelle|Wertetabelle]] - [[Umkehrfunktion_Graph|Graph]] - [[Umkehrfunktion_Term|Term]] - [[Umkehrfunktion_Beispiele|Beispiele]] - [[Umkehrfunktion_Definitions-_und_Wertemenge|Definitions- und Wertemenge]] - [[Umkehrfunktion_Monotonie|Monotoniekriterium]] | ||
Aktuelle Version vom 23. April 2021, 09:55 Uhr
Startseite - Wertetabelle - Graph - Term - Beispiele - Definitions- und Wertemenge - Monotoniekriterium
30px Merke
Eine Funktion Eine Funktion |
Dies heißt, dass bei streng monoton zunehmend mit wachsenden x-Werten auch die y-Werte größer werden. Der Graph geht "bergauf".
Streng monoton abnehmend bedeutet, dass mit wachsenden x-Werten die y-Werte kleiner werden. Der Graph geht "bergab".
30px Merke
Ist eine Funktion |
1. Die Quadratfunktion ist im Intervall ![]-\infty;0]](/images/math/6/7/8/6784e26006f1ff6da806742141c799e4.png) streng monoton abnehmend und im Intervall
streng monoton abnehmend und im Intervall 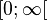 streng monoton zunehmend.
streng monoton zunehmend.
2. Der linke Ast ist für ![x \in ]-\infty;0]](/images/math/3/1/7/317c876687f83055d671c49ca798cdf9.png) umkehrbar
umkehrbar
.
Der rechte Ast ist für 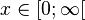 auch umkehrbar.
auch umkehrbar.
3. a) Für den linken Ast ist die Quadratfunktion  eingeschränkt mit
eingeschränkt mit 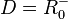 und
und 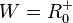 .
.
Die Umkehrfunktion ist 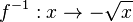 mit
mit 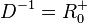 und
und 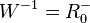 .
.
3. b) Für den rechten Ast ist die Quadratfunktion  eingeschränkt mit
eingeschränkt mit 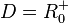 und
und 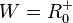
Die Umkehrfunktion 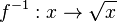 mit
mit 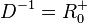 und
und 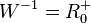 .
.
30px Merke
1. Potenzfunktionen Die Umkehrfunktion ist die n-Wurzelfunktion 2. Potenzfuntkionen Die Umkehrfunktion ist die n-Wurzelfunktion |
Zurück zur Startseite - Wertetabelle - Graph - Term - Beispiele - Definitions- und Wertemenge - Monotoniekriterium
![x_1,x_2 \in [a;b]](/images/math/4/8/9/489a4ad3c2410297428c10a130e7cc95.png) gilt:
gilt: 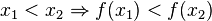
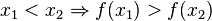
![[a;b]](/images/math/9/4/a/94acf62f087ab3268b2b3fa5a8a7a79c.png) streng monoton, dann ist sie in dem Intervall umkehrbar.
streng monoton, dann ist sie in dem Intervall umkehrbar.
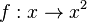 mit
mit 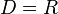 .
.
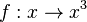 .
.
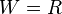
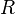 .
.
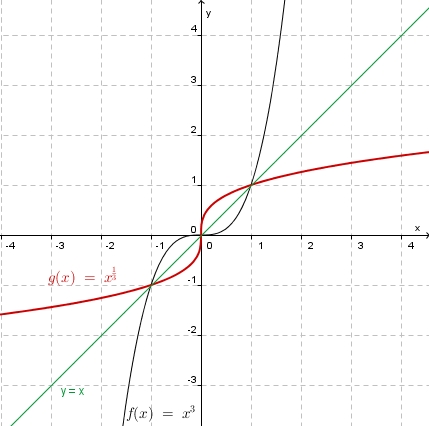
![f^{-1}: x \rightarrow \sqrt[3]x](/images/math/6/d/5/6d504f7ec1cc01d42b5148dbed542bbe.png) mit
mit 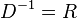 ,
, 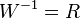
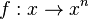 mit ungeraden Exponenten
mit ungeraden Exponenten  sind in
sind in ![f^{-1}: x \rightarrow \sqrt[n]x](/images/math/0/d/4/0d4e6f553537e47e7a11d29f368dd8ad.png) mit
mit 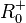 .
.

