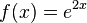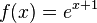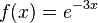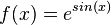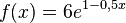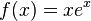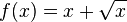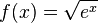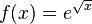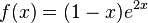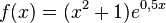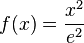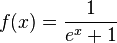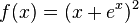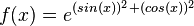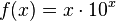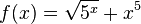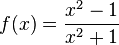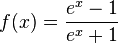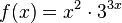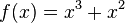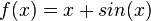M11 Ableitung der Exponentialfunktionen: Unterschied zwischen den Versionen
| Zeile 6: | Zeile 6: | ||
3. [[M10_Verschieben_und_Spiegeln_der_Exponentialkurven|Verschieben und Spiegeln der Exponentialfunktion]] | 3. [[M10_Verschieben_und_Spiegeln_der_Exponentialkurven|Verschieben und Spiegeln der Exponentialfunktion]] | ||
| + | |||
| + | {{Merksatz|MERK=Die Funktion <math>f: R \rightarrow R, f(x) = b\cdot a^x</math> (b ∈ R+\{0}, a ∈ R<sup>+</sup>) heißt '''Exponentialfunktion zur Basis a'''. | ||
| + | <center>[[Datei:Exponentialfunktion 1.jpg|350px]]</center> | ||
| + | Der Graph ist eine Exponentialkurve. }} | ||
| + | |||
| + | Für die Ableitung der Exponentialfunktion zur Basis a geht man auf die Definition zurück:<br> | ||
| + | <math>f'(x) = \lim_{h\to 0}\frac{b^{x+h}-b^x}{h}=\lim_{h\to 0} b^x \cdot \frac{b^h -1}{h}=b^x \cdot \lim_{h\to 0}\frac{b^h - 1}{h}</math> | ||
| + | |||
{{Merksatz|MERK=Die Eulersche Zahl e ist definiert durch den Grenzwert <math>\lim_{h \to 0} \frac{e^h -1}{h}=1</math>. | {{Merksatz|MERK=Die Eulersche Zahl e ist definiert durch den Grenzwert <math>\lim_{h \to 0} \frac{e^h -1}{h}=1</math>. | ||
| Zeile 18: | Zeile 26: | ||
Mit <math>a^x = e^{x \cdot ln(a)}</math> und der Kettenregel erhält man <br> | Mit <math>a^x = e^{x \cdot ln(a)}</math> und der Kettenregel erhält man <br> | ||
<center><math> (a^x)' = ln(a) \cdot a^x</math>.</center> }} | <center><math> (a^x)' = ln(a) \cdot a^x</math>.</center> }} | ||
| + | |||
| + | {{Aufgaben-blau|1|2=Bestimmen Sie die erste Ableitung<br> | ||
| + | a) <math>f(x) = e^{2x}</math><br> | ||
| + | b) <math>f(x) = e^{x+1}</math><br> | ||
| + | c) <math>f(x) = e^{-3x}</math><br> | ||
| + | d) <math>f(x) = e^{sin(x)}</math><br> | ||
| + | e) <math>f(x) = 6e^{1-0,5x}</math><br> | ||
| + | f) <math>f(x) = xe^{x}</math><br> | ||
| + | g) <math>f(x) = x + \sqrt x</math><br> | ||
| + | h) <math>f(x) = \sqrt {e^x}</math><br> | ||
| + | i) <math>f(x) = e^{\sqrt x}</math><br> | ||
| + | j) <math>f(x) = (1-x)e^{2x}</math><br> | ||
| + | k) <math>f(x) = (x^2 + 1)e^{0,5x}</math><br> | ||
| + | l) <math>f(x) = \frac{x^2}{e^2}</math><br> | ||
| + | m) <math>f(x) = \frac{1}{e^x + 1}</math><br> | ||
| + | n) <math>f(x) = (x + e^x)^2</math><br> | ||
| + | o) <math>f(x) = e^{(sin(x))^2 + (cos(x))^2}</math><br> | ||
| + | p) <math>f(x) = e^{2x}</math><br> | ||
| + | q) <math>f(x) = x \cdot 10^x</math><br> | ||
| + | r) <math>f(x) = \sqrt {5^x} + x^5</math><br> | ||
| + | s) <math>f(x) = \frac{x^2 - 1}{x^2 + 1}</math><br> | ||
| + | t) <math>f(x) = \frac{e^x -1}{e^x + 1}</math><br> | ||
| + | u) <math>f(x) = x^2 \cdot 3^{3x}</math><br> | ||
| + | v) <math>f(x) = x^3 + x^2</math><br> | ||
| + | w) <math>f(x) = x + sin(x)</math><br> | ||
| + | x) <math>f(x) = |x-1|</math> }} | ||
| + | |||
| + | {{Lösung versteckt|1= Beachten Sie die Ableitungsregeln, insbesondere die Kettenregel. <br> | ||
| + | a) <math>f'(x) = 2e^{2x}</math><br> | ||
| + | b) <math>f'(x) = e^{x+1}</math><br> | ||
| + | c) <math>f'(x) = -3e^{-3x}</math><br> | ||
| + | d) <math>f'(x) = cos(x)\cdot e^{sin(x)}</math><br> | ||
| + | e) <math>f'(x) = -3e^{1-0,5x}</math><br> | ||
| + | f) <math>f'(x) = e^{x} + x e^x = (x+1)e^x</math><br> | ||
| + | g) <math>f'(x) = 1 + \frac{1}{2\sqrt x}</math><br> | ||
| + | h) <math>f'(x) = \frac{e^x}{2\sqrt {e^x}}=\frac{1}{2}e^x</math><br> | ||
| + | Dies hätte man auch erhalten, wenn man <math>f(x) = \sqrt {e^x}= (e^x)^{\frac{1}{2}}</math> ableitet.<br> | ||
| + | i) <math>f'(x) = e^{\sqrt x}\cdot \frac{1}{2\sqrt x} =\frac{e^{\sqrt x}}{2\sqrt x}</math><br> | ||
| + | j) <math>f'(x) = -1e^{2x} + 2(1-x)e^{2x}=(1-2x)e^{2x}</math><br> | ||
| + | k) <math>f'(x) = 2x e^{0,5x} + 0,5(x^2 + 1)e^{0,5x}=(0,5x^2 + 2x +0,5)e^{0,5x}</math><br> | ||
| + | l) <math>f'(x) = \frac{2x}{e^2} </math> - Beachte e<sup>2</sup> ist eine Zahl und hier steht keine Exponentialfunktion!<br> | ||
| + | m) <math>f'(x) = \frac{-e^x}{(e^x + 1)^2}</math><br> | ||
| + | n) <math>f'(x) = 2(x + e^x)(1+e^x)</math><br> | ||
| + | o) <math>f'(x) = (e^{(sin(x))^2 + (cos(x))^2})=e^1 = 0</math><br> | ||
| + | p) <math>f(x) = 2e^{2x}</math><br> | ||
| + | q) <math>f'(x) = 1\cdot 10^x + x \cdot 10^x \cdot ln(10) = 10^x (1 + ln(10)x)</math><br> | ||
| + | r) <math>f'(x) = (\sqrt {5^x} + x^5)'=(5^{\frac{x}{2}} + x^5)' = (e^{ln(5)\cdot \frac{x}{2}} + x^5)'=\frac{ln(5)}{2 }e^{ln(5)\cdot \frac{x}{2}} + 5x^4=\frac{ln(5)}{2}\sqrt {5^x} + 5x^4 </math><br> | ||
| + | s) <math>f'(x) = \frac{2x\cdot(x^2+1)-2x\cdot (x^2-1)}{(x^2 + 1)^2}=\frac{4x}{(x^2+1)^2}</math><br> | ||
| + | t) <math>f'(x) = \frac{e^x(e^x+1)- e^x(e^x-1)}{(e^x + 1)^2}=\frac{2e^x}{(e^x+1)^2}</math><br> | ||
| + | u) <math>f'(x) = 2x \cdot e^{3x}+3x^2e^{3x}</math><br> | ||
| + | v) <math>f'(x) = 3x^2 + 2x</math><br> | ||
| + | w) <math>f(x) = 1 + cos(x)</math><br> | ||
| + | x) <math>f(x) = |x-1|</math> <br> | ||
| + | Bei x = 1 hat die Funktion einen Knick. Für x < 1 ist f(x) = -x + 1 und f'(x) = -1; für x < 1 ist f(x) = x -1 und f'(x) = 1.}} | ||
Version vom 18. März 2021, 16:44 Uhr
Zur Wiederholung:
2. Eigenschaften der Exponentialfunktion
3. Verschieben und Spiegeln der Exponentialfunktion
|
Merke:
Die Funktion 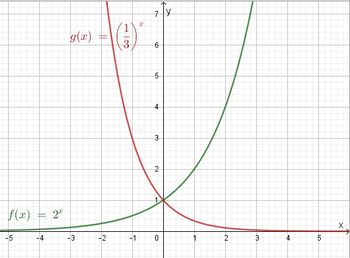 Der Graph ist eine Exponentialkurve. |
Für die Ableitung der Exponentialfunktion zur Basis a geht man auf die Definition zurück:
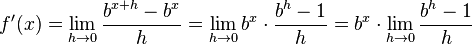
|
Merke:
Die Eulersche Zahl e ist definiert durch den Grenzwert Dies hat zur Folge, dass die Exponentialfunktion zur Basis e 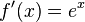 oder oder 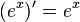 hat. Jede Funktion
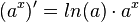 . . |
Beachten Sie die Ableitungsregeln, insbesondere die Kettenregel.
a) 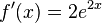
b) 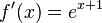
c) 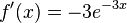
d) 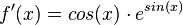
e) 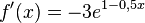
f) 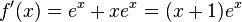
g) 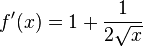
h) 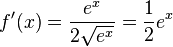
Dies hätte man auch erhalten, wenn man 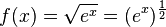 ableitet.
ableitet.
i) 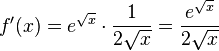
j) 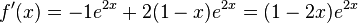
k) 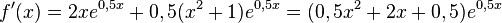
l) 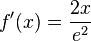 - Beachte e2 ist eine Zahl und hier steht keine Exponentialfunktion!
- Beachte e2 ist eine Zahl und hier steht keine Exponentialfunktion!
m) 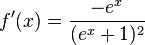
n) 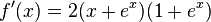
o) 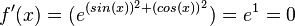
p) 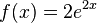
q) 
r) 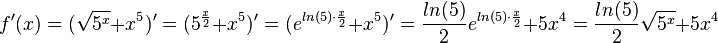
s) 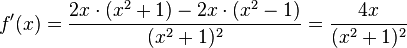
t) 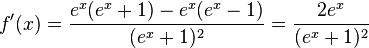
u) 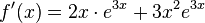
v) 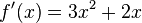
w) 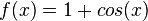
x) 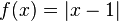

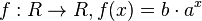 (b ∈ R+\{0}, a ∈ R+) heißt Exponentialfunktion zur Basis a.
(b ∈ R+\{0}, a ∈ R+) heißt Exponentialfunktion zur Basis a.
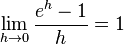 .
.
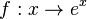 mit D = R und W = R+ die Ableitung
mit D = R und W = R+ die Ableitung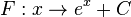 ist Stammfunktion von
ist Stammfunktion von  .
.
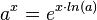 und der Kettenregel erhält man
und der Kettenregel erhält man