Umkehrfunktion Monotonie: Unterschied zwischen den Versionen
| Zeile 54: | Zeile 54: | ||
und der rechte Ast <math>x \in [0;\infty[</math> ist ebenso umkehrbar. | und der rechte Ast <math>x \in [0;\infty[</math> ist ebenso umkehrbar. | ||
| − | Für den linken Ast ist <math>D = R^-_0 <math> und <math> W = R^+_0</math>. <br> | + | Für den linken Ast ist <math>D = R^-_0 </math> und <math> W = R^+_0</math>. <br> |
Umkehrfunktion <math>f^{-1}:x \rightarrow -sqrt x</math> mit <math>D^{-1} = R^+_0 </math> und <math>W^{-1} = R^-_0</math>. | Umkehrfunktion <math>f^{-1}:x \rightarrow -sqrt x</math> mit <math>D^{-1} = R^+_0 </math> und <math>W^{-1} = R^-_0</math>. | ||
| − | Für den rechten Ast ist <math>D = R^+_0 <math> und <math> W = R^+_0</math><br> | + | Für den rechten Ast ist <math>D = R^+_0 </math> und <math> W = R^+_0</math><br> |
Umkehrfunktion <math>f^{-1}:x \rightarrow sqrt x</math> mit <math>D^{-1} = R^+_0 </math> und <math>W^{-1} = R^+_0</math>. | Umkehrfunktion <math>f^{-1}:x \rightarrow sqrt x</math> mit <math>D^{-1} = R^+_0 </math> und <math>W^{-1} = R^+_0</math>. | ||
}} | }} | ||
Version vom 23. Mai 2012, 14:09 Uhr
Startseite - Wertetabelle - Graph - Term - Beispiele - Definitions- und Wertemenge - Monotoniekriterium
30px Merke
Eine Funktion Eine Funktion |
30px Aufgabe
|
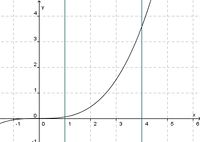 (streng monoton steigend) (!streng monoton fallend) (!weder noch)
(streng monoton steigend) (!streng monoton fallend) (!weder noch)
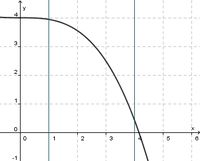 (!streng monoton steigend) (streng monoton fallend) (!weder noch)
(!streng monoton steigend) (streng monoton fallend) (!weder noch)
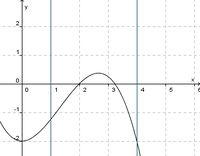 (!streng monoton steigend) (!streng monoton fallend) (weder noch)
(!streng monoton steigend) (!streng monoton fallend) (weder noch)
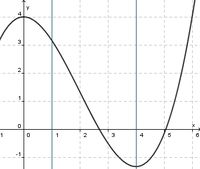 (!streng monoton steigend) (streng monoton fallend) (!weder noch)
(!streng monoton steigend) (streng monoton fallend) (!weder noch)
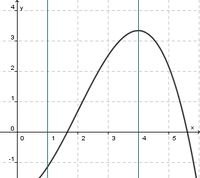 (streng monoton steigend) (!streng monoton fallend) (!weder noch)
(streng monoton steigend) (!streng monoton fallend) (!weder noch)
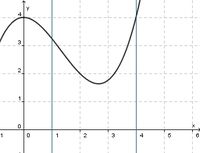 (!streng monoton steigend) (!streng monoton fallend) (weder noch)
(!streng monoton steigend) (!streng monoton fallend) (weder noch)
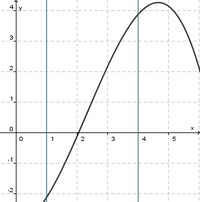 (streng monoton steigend) (!streng monoton fallend) (!weder noch)
(streng monoton steigend) (!streng monoton fallend) (!weder noch)
30px Merke
Ist eine Funktion Gib jeweils die Umkehrfunktion an. |
30px Aufgabe
Wo ist die Quadratfunktion |
Die Quadratfunktion ist im Intervall ![]-\infty;0]](/images/math/6/7/8/6784e26006f1ff6da806742141c799e4.png) streng monoton abnehmend und im Intervall
streng monoton abnehmend und im Intervall 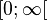 streng monoton zunehmend.
streng monoton zunehmend.
Somit ist der linke Ast ![x \in ]-\infty;0]](/images/math/3/1/7/317c876687f83055d671c49ca798cdf9.png) umkehrbar
umkehrbar
und der rechte Ast 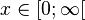 ist ebenso umkehrbar.
ist ebenso umkehrbar.
Für den linken Ast ist 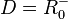 und
und 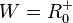 .
.
Umkehrfunktion 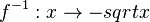 mit
mit 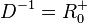 und
und 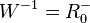 .
.
Für den rechten Ast ist 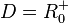 und
und 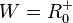
Umkehrfunktion 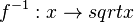 mit
mit 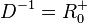 und
und 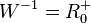 .
.
 heißt streng monoton zunehmend im Intervall [a;b], wenn für alle
heißt streng monoton zunehmend im Intervall [a;b], wenn für alle ![x_1,x_2 \in [a;b]](/images/math/4/8/9/489a4ad3c2410297428c10a130e7cc95.png) gilt:
gilt: 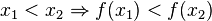
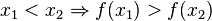
![[a;b]](/images/math/9/4/a/94acf62f087ab3268b2b3fa5a8a7a79c.png) streng monoton, dann ist sie in dem Intervall umkehrbar.
streng monoton, dann ist sie in dem Intervall umkehrbar.
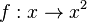 mit
mit 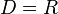 umkehrbar?
umkehrbar?

