Umkehrfunktion Monotonie: Unterschied zwischen den Versionen
| Zeile 19: | Zeile 19: | ||
{{Aufgabe| | {{Aufgabe| | ||
| − | Teste | + | Teste dein Wissen auf dieser [[Monotonie_Test|Seite]] |
}} | }} | ||
| − | |||
| − | |||
| − | |||
| − | [ | + | {{Merke| |
| − | + | Ist eine Funktion <math> f </math> im Intervall <math>[a;b]</math> streng monoton, dann ist sie in dem Intervall umkehrbar. | |
| + | }} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | {{Aufgabe|Betrachte nun die Quadratfunktion <math> f: x\rightarrow x^2</math> mit <math>D = R</math>. | |
| − | + | ||
| − | + | 1. Wo ist die Quadratfunktion streng monoton abnehmend? Wo ist sie streng monoton zunehmend? | |
| − | + | ||
| − | + | 2. In welchen Intervallen ist die Quadratfunktion umkehrbar? | |
| − | + | ||
| − | + | 3. Gib für beide Intervalle die Umkehrfunktionen an. Zeichne jeweils die Graphen von eingeschränkter Funktion und Umkehrfunktion. | |
| + | }} | ||
| + | {{Lösung versteckt| | ||
| + | 1. Die Quadratfunktion ist im Intervall <math>]-\infty;0]</math> streng monoton abnehmend und im Intervall <math> [0;\infty[</math> streng monoton zunehmend. | ||
| − | + | 2. Der linke Ast für <math>x \in ]-\infty;0]</math> umkehrbar <br>. | |
| − | + | Der rechte Ast ist für <math>x \in [0;\infty[</math> auch umkehrbar. | |
| + | |||
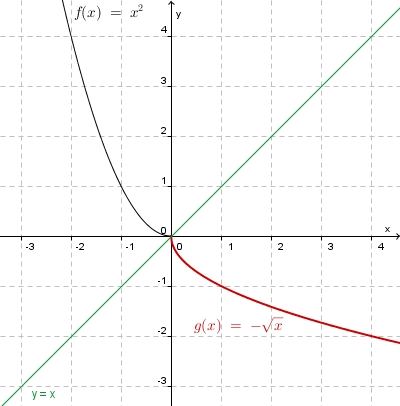
| + | 3. a) Für den linken Ast ist die Quadratfunktion <math>f</math> eingeschränkt mit <math>D = R^-_0 </math> und <math> W = R^+_0</math>. <br> | ||
| + | Die Umkehrfunktion ist <math>f^{-1}:x \rightarrow -sqrt x</math> mit <math>D^{-1} = R^+_0 </math> und <math>W^{-1} = R^-_0</math>. | ||
| + | |||
| + | [[Bild:Umkfkt_quafkt_-.jpg]] | ||
| + | |||
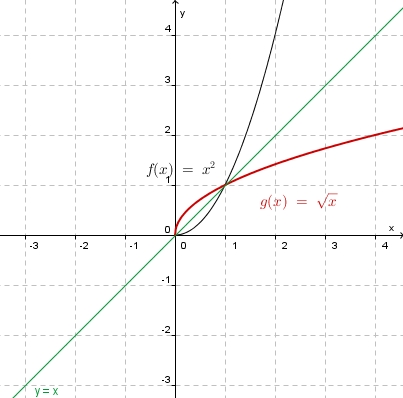
| + | 3. b) Für den rechten Ast ist die Quadratfunktion <math>f</math> eingeschränkt mit <math>D = R^+_0 </math> und <math> W = R^+_0</math><br> | ||
| + | Die Umkehrfunktion <math>f^{-1}:x \rightarrow sqrt x</math> mit <math>D^{-1} = R^+_0 </math> und <math>W^{-1} = R^+_0</math>. | ||
| + | |||
| + | [[Bild:Umkfkt_quafkt_+.jpg]] | ||
}} | }} | ||
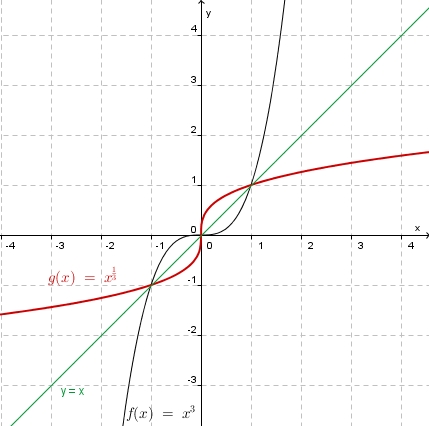
| + | {{Aufgabe|Betrachte nun die Potenzfunktion <math> f: x \rightarrow x^3</math>. | ||
| + | 1. Gib Definitions- und Wertemenge an. | ||
| − | + | 2. Zeichne den Graphen der Funktion <math>f</math>. | |
| − | + | 3. Wo ist die Funktion streng monoton? | |
| − | + | 4. Bestimme die Umkehrfunktion zu f. Zeichne sie in das Diagramm von 2. | |
| + | }} | ||
| − | + | {{Lösung versteckt| | |
| − | + | 1. <math> D = R</math>, <math>W = R</math> | |
| − | + | 2. [[Bild:Umkfkt_kubikfkt.jpg]] | |
| − | + | ||
| − | + | 3. F ist streng monoton zunehmend in ganz <math>R</math>. | |
| − | + | 4. <math>f^{-1}: x \rightarrow \sqrt[3]x</math> mit <math> D^{-1} = R</math>, <math>W^{-1} = R</math> | |
| − | + | ||
| − | |||
}} | }} | ||
| + | |||
| + | {{Merke| | ||
| + | 1. Potenzfunktionen <math>f: x \rightarrow x^n</math> mit ungeraden Exponenten <math>n</math> sind in <math>R</math> umkehrbar. | ||
| + | |||
| + | Die Umkehrfunktion ist die n-Wurzelfunktion <math>f^{-1}: x \rightarrow \sqrt[n]x</math> mit <math> D^{-1} = R</math>, <math>W^{-1} = R</math>. | ||
| + | |||
| + | 2. Potenzfuntkionen <math>f: x \rightarrow x^n</math> mit geraden Exponenten <math>n</math> sind in <math>R</math> nicht umkehrbar. Sie müssen eingeschränkt werden, z.B. auf <math>R^+_0</math>. | ||
| + | |||
| + | Die Umkehrfunktion ist die n-Wurzelfunktion <math>f^{-1}: x \rightarrow \sqrt[n]x</math> mit <math> D^{-1} = R^+_0</math>, <math>W^{-1} = R^+_0</math>. | ||
| + | }} | ||
| + | |||
| + | ---- | ||
| + | Zurück zur [[Die_Umkehrfunktion|Startseite]] - [[Umkehrfunktion_Wertetabelle|Wertetabelle]] - [[Umkehrfunktion_Graph|Graph]] - [[Umkehrfunktion_Term|Term]] - [[Umkehrfunktion_Beispiele|Beispiele]] - [[Umkehrfunktion_Definitions-_und_Wertemenge|Definitions- und Wertemenge]] - [[Umkehrfunktion_Monotonie|Monotoniekriterium]] | ||
Version vom 23. Mai 2012, 19:00 Uhr
Startseite - Wertetabelle - Graph - Term - Beispiele - Definitions- und Wertemenge - Monotoniekriterium
30px Merke
Eine Funktion Eine Funktion |
Dies heißt, dass bei streng monoton zunehmend mit wachsenden x-Werten auch die y-Werte größer werden. Der Graph geht "bergauf".
Streng monoton abnehmend bedeutet, dass mit wachsenden x-Werten die y-Werte kleiner werden. Der Graph geht "bergab".
30px Aufgabe
|
30px Merke
Ist eine Funktion |
30px Aufgabe
Betrachte nun die Quadratfunktion 1. Wo ist die Quadratfunktion streng monoton abnehmend? Wo ist sie streng monoton zunehmend? 2. In welchen Intervallen ist die Quadratfunktion umkehrbar? 3. Gib für beide Intervalle die Umkehrfunktionen an. Zeichne jeweils die Graphen von eingeschränkter Funktion und Umkehrfunktion.
|
1. Die Quadratfunktion ist im Intervall ![]-\infty;0]](/images/math/6/7/8/6784e26006f1ff6da806742141c799e4.png) streng monoton abnehmend und im Intervall
streng monoton abnehmend und im Intervall 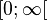 streng monoton zunehmend.
streng monoton zunehmend.
2. Der linke Ast für ![x \in ]-\infty;0]](/images/math/3/1/7/317c876687f83055d671c49ca798cdf9.png) umkehrbar
umkehrbar
.
Der rechte Ast ist für 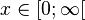 auch umkehrbar.
auch umkehrbar.
3. a) Für den linken Ast ist die Quadratfunktion  eingeschränkt mit
eingeschränkt mit 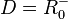 und
und 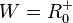 .
.
Die Umkehrfunktion ist 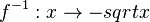 mit
mit 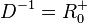 und
und 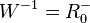 .
.
3. b) Für den rechten Ast ist die Quadratfunktion  eingeschränkt mit
eingeschränkt mit 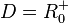 und
und 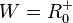
Die Umkehrfunktion 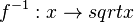 mit
mit 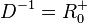 und
und 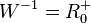 .
.
30px Aufgabe
Betrachte nun die Potenzfunktion 1. Gib Definitions- und Wertemenge an. 2. Zeichne den Graphen der Funktion 3. Wo ist die Funktion streng monoton? 4. Bestimme die Umkehrfunktion zu f. Zeichne sie in das Diagramm von 2. |
30px Merke
1. Potenzfunktionen Die Umkehrfunktion ist die n-Wurzelfunktion 2. Potenzfuntkionen Die Umkehrfunktion ist die n-Wurzelfunktion |
Zurück zur Startseite - Wertetabelle - Graph - Term - Beispiele - Definitions- und Wertemenge - Monotoniekriterium
![x_1,x_2 \in [a;b]](/images/math/4/8/9/489a4ad3c2410297428c10a130e7cc95.png) gilt:
gilt: 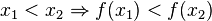
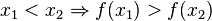
![[a;b]](/images/math/9/4/a/94acf62f087ab3268b2b3fa5a8a7a79c.png) streng monoton, dann ist sie in dem Intervall umkehrbar.
streng monoton, dann ist sie in dem Intervall umkehrbar.
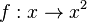 mit
mit 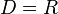 .
.
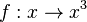 .
.
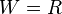
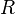 .
.
![f^{-1}: x \rightarrow \sqrt[3]x](/images/math/6/d/5/6d504f7ec1cc01d42b5148dbed542bbe.png) mit
mit 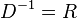 ,
, 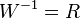
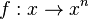 mit ungeraden Exponenten
mit ungeraden Exponenten  sind in
sind in ![f^{-1}: x \rightarrow \sqrt[n]x](/images/math/0/d/4/0d4e6f553537e47e7a11d29f368dd8ad.png) mit
mit 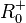 .
.

