M11 Ableitung der Exponentialfunktionen: Unterschied zwischen den Versionen
Aus RSG-Wiki
(Die Seite wurde neu angelegt: „'''Zur Wiederholung:''' 1. Die Exponentialfunktion 2. M10_Eigenschaften_der_Exponentialfunktion|Eigenschaften der Exponenti…“) |
Version vom 18. März 2021, 15:46 Uhr
Zur Wiederholung:
2. Eigenschaften der Exponentialfunktion
3. Verschieben und Spiegeln der Exponentialfunktion
|
Merke:
Die Eulersche Zahl e ist definiert durch den Grenzwert Dies hat zur Folge, dass die Exponentialfunktion zur Basis e 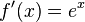 oder oder 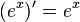 Mit 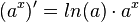 . . |

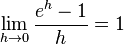 .
.
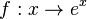 mit D = R und W = R+ die Ableitung
mit D = R und W = R+ die Ableitung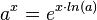 und der Kettenregel erhält man
und der Kettenregel erhält man 
