Die Umkehrfunktion: Unterschied zwischen den Versionen
(→Beispiele) |
|||
| Zeile 22: | Zeile 22: | ||
Mehr zum Funktionsbegriff findest du auf [http://wikis.zum.de/medienvielfalt/Funktionen_Einstieg/Der_Funktionsbegriff dieser Seite]. | Mehr zum Funktionsbegriff findest du auf [http://wikis.zum.de/medienvielfalt/Funktionen_Einstieg/Der_Funktionsbegriff dieser Seite]. | ||
| + | |||
| + | Wir wollen nun Betrachtungen zur Umkehrfunktion anstellen. Wie erhält man eine Umkehrfunktion? | ||
| + | Mit Hilfe | ||
| + | |||
| + | * der [[Umkehrfunktion_Wertetabelle|Wertetabelle]] | ||
| + | * des [[Umkehrfunktion_Graph|Graphen]] | ||
| + | * des [[Umkehrfunktion_Term|Terms]] | ||
| + | |||
| + | Weiter gibt es dann [[Umkehrfunktion_Beispiele|Beispiele]]. | ||
| + | |||
| + | Gibt es immer eine Umkehrfunktion? Dazu muss [[Umkehrfunktion_Definitions-_und_Wertemenge|Definitions- und Wertemenge]] betrachten. <br> | ||
| + | Mit dem [[Umkehrfunktion_Monotinie|Monotoniekriterium]] gibt es ein einfaches Mittel die Umkehrfunktion zu bestimmen. | ||
| + | |||
| + | |||
=Umkehrfunktion mit der Wertetabelle= | =Umkehrfunktion mit der Wertetabelle= | ||
Version vom 22. Mai 2012, 10:56 Uhr
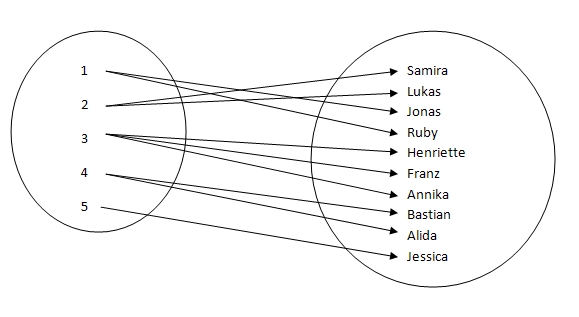
In der letzten Mathearbeit haben
Samira und Lukas eine 2, Jonas und Ruby eine 1, Henriette, Franz und Annika eine 3, Bastian und Alida eine 4 und Jessica eine 5.
In einem Pfeildiagramm schaut das so aus:
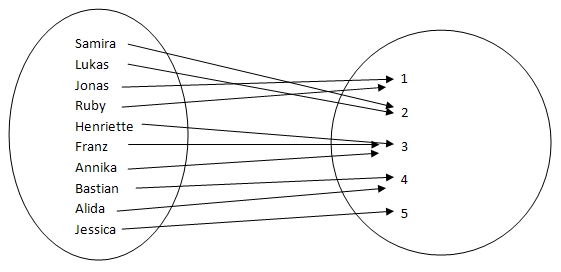
Jedem Schüler wird die Note in der Mathearbeit zugeordnet. Jeder Pfeil endet genau bei einer Note.
30px Merke
Man spricht von einer Funktion, wenn jedem Element einer Menge genau ein Element einer anderen Menge zugeordnet wird. |
In unserem Beispiel wird jedem Schüler genau eine Note zugeordnet. Es handelt sich bei dieser Zuordnung um eine Funktion.
30px Aufgabe
Gib nun umgekehrt die Zuordnung an, die jeder Note den Schüler zuordnet, der die Note geschrieben hat. |
Hier wird jeder Note teils mehrere Schüler zugeordnet. Von einer Note gehen mehrere Pfeile aus. Es handelt sich hier um keine Funktion!.
Mehr zum Funktionsbegriff findest du auf dieser Seite.
Wir wollen nun Betrachtungen zur Umkehrfunktion anstellen. Wie erhält man eine Umkehrfunktion? Mit Hilfe
- der Wertetabelle
- des Graphen
- des Terms
Weiter gibt es dann Beispiele.
Gibt es immer eine Umkehrfunktion? Dazu muss Definitions- und Wertemenge betrachten.
Mit dem Monotoniekriterium gibt es ein einfaches Mittel die Umkehrfunktion zu bestimmen.
Umkehrfunktion mit der Wertetabelle
30px Aufgabe
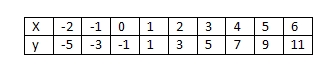
Betrachte die Funktion |
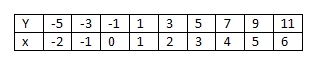
Vertauscht man nun die Bezeichnungen 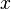 und
und 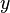 , dann hat man wieder die Wertetabelle in der bekannten Form:
, dann hat man wieder die Wertetabelle in der bekannten Form:

Umkehrfunktion mit dem Graphen
Mit dem Graph einer Funktion kann man leicht zu einem 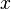 -Wert den
-Wert den 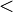 -Wert bestimmen, indem man z.B. bei
-Wert bestimmen, indem man z.B. bei 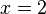 von der x-Achse senkrecht nach oben geht bis man den Graph trifft. In diesem Punkt geht man waagrecht zur y-Achse und bekokmmt den
von der x-Achse senkrecht nach oben geht bis man den Graph trifft. In diesem Punkt geht man waagrecht zur y-Achse und bekokmmt den 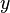 -Wert. Für das Beispiel ist dann
-Wert. Für das Beispiel ist dann 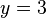 .
.
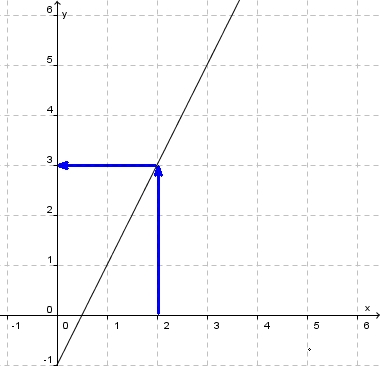
Geht man diesen Weg umgekehrt, also von 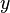 -Wert auf der y-Achse (z.B.
-Wert auf der y-Achse (z.B. 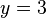 ) waagrecht bis zum Graph und von diesem Punkt senkrecht nach unten zur x-Achse, dann erhält man den
) waagrecht bis zum Graph und von diesem Punkt senkrecht nach unten zur x-Achse, dann erhält man den 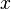 -Wert. Im Beispiel
-Wert. Im Beispiel 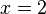 .
.
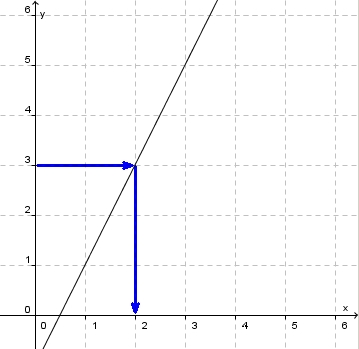
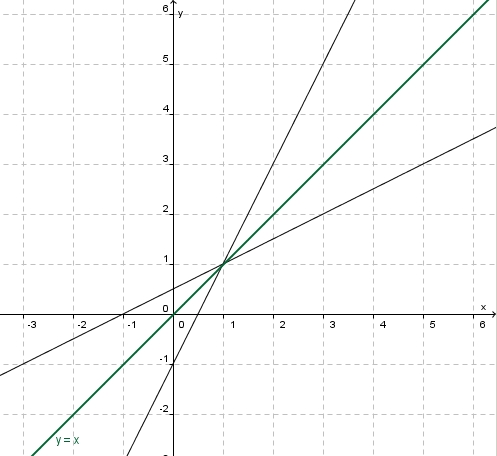
Jetzt ist nur ungewohnt, dass man von der y-Achse losgeht und über den Graph zur x-Achse kommt. Vertauscht man x- und y-Achse, dann hat man wieder das gewohnte Bild.
x- und y-Achse kann man durch eine Achsenspiegelung an der Geraden y = x (Winkelhalbierende des I. und III. Quadranten, 1. Mediane) vertauschen. Natürlich wird dann der Graph der Funktion 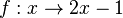 auch gespiegelt und man erhält den Graph der Funktion
auch gespiegelt und man erhält den Graph der Funktion 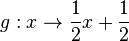 .
.
30px Aufgabe
Zeichne in den Graphen die Pfeile, die Welchen |
30px Merke
So erhältst du den Graphen der Umkehrfunktion 1. Zeichne den Graphen der Funktion 2. Zeichne die Gerade 3. Spiegele den Graphen der Funktion |
Umkehrfunktion mit dem Term
Beim Graph hast du gesehen, dass beim Bilden des Graphen der Umkehrfunktion wieder eine Gerade entsteht. Aus dem Diagramm kannst du die Geradengleichung ablesen.
30px Aufgabe
1. Wie vertauscht man x- und y- Achse im Term? 2. Löse die Gleichung |
1. Man vertauscht im Term x und y.
2.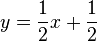
30px Merke
So findest du den Term der Umkehrfunktion:
2. Vertausche x und y
3. Löse nach y auf
|
Damit erhältst du die Gleichung der Umkehrfunktion. Da diese Funktion sehr eng mit der Funktion  zusammenhängt, schreibt man meist
zusammenhängt, schreibt man meist 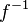 für sie. Damit ist zur Funktion
für sie. Damit ist zur Funktion 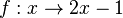 die Umkehrfunktion
die Umkehrfunktion 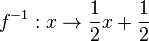 .
.
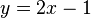 zugeordnet. Stelle zuerst eine Wertetabelle auf und danach stelle die Wertetabelle für die Umkehrfunktion auf.
zugeordnet. Stelle zuerst eine Wertetabelle auf und danach stelle die Wertetabelle für die Umkehrfunktion auf.
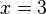 den
den 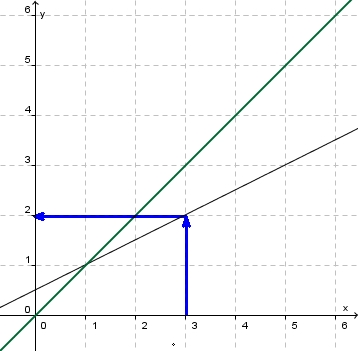
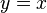 in das Diagramm.
in das Diagramm.
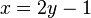 nach y auf.
nach y auf.

