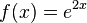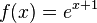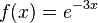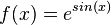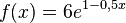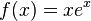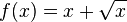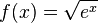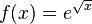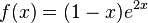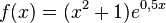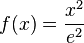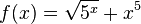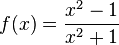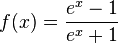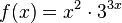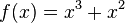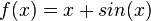M11 Ableitung der Exponentialfunktionen
Zur Wiederholung:
2. Eigenschaften der Exponentialfunktion
3. Verschieben und Spiegeln der Exponentialfunktion
|
Merke:
Die Funktion 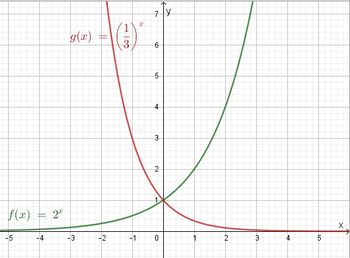 Der Graph ist eine Exponentialkurve. |
Für die Ableitung der Exponentialfunktion zur Basis a geht man auf die Definition zurück:
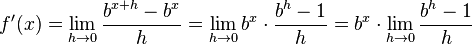
|
Merke:
Die Eulersche Zahl e ist definiert durch den Grenzwert Dies hat zur Folge, dass die Exponentialfunktion zur Basis e 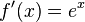 oder oder 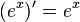 hat. Jede Funktion
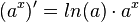 . . |
Beachten Sie die Ableitungsregeln, insbesondere die Kettenregel.
a) 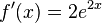
b) 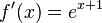
c) 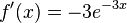
d) 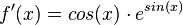
e) 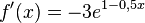
f) 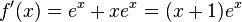
g) 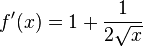
h) 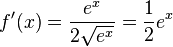
Dies hätte man auch erhalten, wenn man 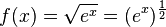 ableitet.
ableitet.
i) 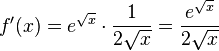
j) 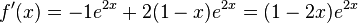
k) 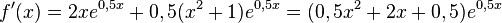
l) 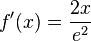 - Beachte e2 ist eine Zahl und hier steht keine Exponentialfunktion!
- Beachte e2 ist eine Zahl und hier steht keine Exponentialfunktion!
m) 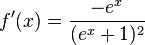
n) 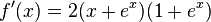
o) 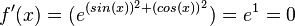
p) 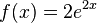
q) 
r) 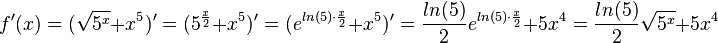
s) 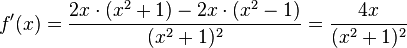
t) 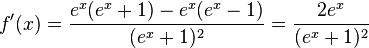
u) 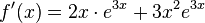
v) 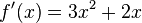
w) 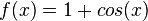
x) 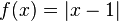

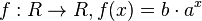 (b ∈ R+\{0}, a ∈ R+) heißt Exponentialfunktion zur Basis a.
(b ∈ R+\{0}, a ∈ R+) heißt Exponentialfunktion zur Basis a.
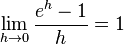 .
.
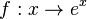 mit D = R und W = R+ die Ableitung
mit D = R und W = R+ die Ableitung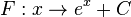 ist Stammfunktion von
ist Stammfunktion von  .
.
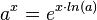 und der Kettenregel erhält man
und der Kettenregel erhält man