Abiturwissen Mathematik: Unterschied zwischen den Versionen
(→Analysis) |
(→Geometrie) |
||
| Zeile 82: | Zeile 82: | ||
| − | Um einen senkrechten Vektor zu einem gegebenen Vektor <math> \vec{n}</math> zu finden, gibt es | + | Um einen senkrechten Vektor zu einem gegebenen Vektor <math> \vec{n}</math> zu finden, gibt es folgendem Trick:<br> |
1. Eine Komponente des Normalenvektors 0 setzen. <br> | 1. Eine Komponente des Normalenvektors 0 setzen. <br> | ||
2. Die anderen beiden Komponenten vertauschen.<br> | 2. Die anderen beiden Komponenten vertauschen.<br> | ||
3. Eine der beiden vertauschten Komponenten negieren. | 3. Eine der beiden vertauschten Komponenten negieren. | ||
Aktuelle Version vom 8. Mai 2020, 10:51 Uhr
Inhaltsverzeichnis |
Was man im Abitur wissen sollte
Es kommen im Abitur viele Sachen aus den unteren Klassen vor. Mit den Links auf der Seite
kann man vorhandene Lücken aufarbeiten.
Bei Mathematik_Q11 und Mathematik_Q12 findet man viel zum aktuellen Stoff!
Im Weiteren findet ihr diverse Inhalte, die man für das Abitur auch noch wiederholen kann:
Abituraufgaben
- Abituraufgaben der letzten Jahre - Aufgaben, Lösungen, Videos in denen ein Lehrer die Aufgaben vorrechnet. Man muss sich aber vorher anmelden.
- Die Aufgaben beim ISB
Analysis
- Einfluss der Parameter
bei quadratischen Funktionen Scheitelform und allgemeine Form
bei trigonometrischen Funktionen
bei Wurzelfunktionen
- Das logarithmische Integrieren als Video oder hier (Seite 1) und Aufgaben 1- 12
Stochastik
- Pfadregeln:
Die Pfadregeln
Die Pfadregeln mit Beispielen
Aufgaben 1 und 2 mit Lösungen, 3
Geometrie
Aufgaben zur Lagebeziehung Gerade - Ebene
Nun noch zum Üben ein paar Aufgaben zur Lagebezeihung zweier Ebenen
Abstands- und Winkelbestimmungen
Als Stützvektor nimmt man den Ortsvektor des gegebenen Punktes P. Nun braucht man noch zwei Richtungsvektoren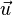 
und 
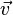. Das Vektorprodukt hilft uns hier nicht weiter. Man erhält die Richtungsvektoren mit folgendem Trick:
1. Eine Komponente des Normalenvektors 0 setzen.
2. Die anderen beiden Komponenten vertauschen.
3. Eine der beiden vertauschten Komponenten negieren.
Beispiel: P(5;1;2) und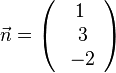 
1. x1- und x2-Komponente werden 0 gesetzt.
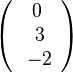und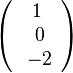 
2. Die anderen beiden Komponenten werden jeweils vertauscht.
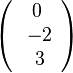und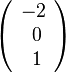 
3. Eine der beiden vertauschen Komponenten wird negiert.
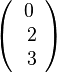und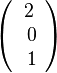 
Damit sind die Richtungsvektoren der Ebene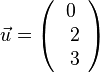 
und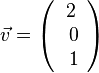 
.
Dies liefert die Parametergleichung der Ebene E: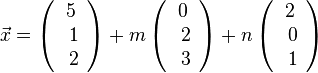 
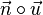und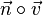 
jeweils 0 sind, also stehen die Richtungsvektoren 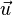und 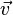senkrecht zum Normalenvektor 
.
Um einen senkrechten Vektor zu einem gegebenen Vektor
1. Eine Komponente des Normalenvektors 0 setzen.
2. Die anderen beiden Komponenten vertauschen.
3. Eine der beiden vertauschten Komponenten negieren.
